[TS] CH02. 실습2(추세모형)

Time Series
Author

김보람

Published

October 2, 2023

해당 자료는 전북대학교 이영미 교수님 2023고급시계열분석 자료임

패키지 설치

############## package
library(lmtest) ##DW test
library(ggplot2)
library(lubridate)
library(gridExtra)
options(repr.plot.width = 15, repr.plot.height = 8)

삼각함수 그려보기

- \(sin(x)\): 주기가 2\(\pi\)인 주기 함수

x <- seq(0,48,0.01)
plot(x, sin(x), type='l')
abline(h=0, lty=2)
abline(v=seq(0,48, by = 2*pi), lty=2)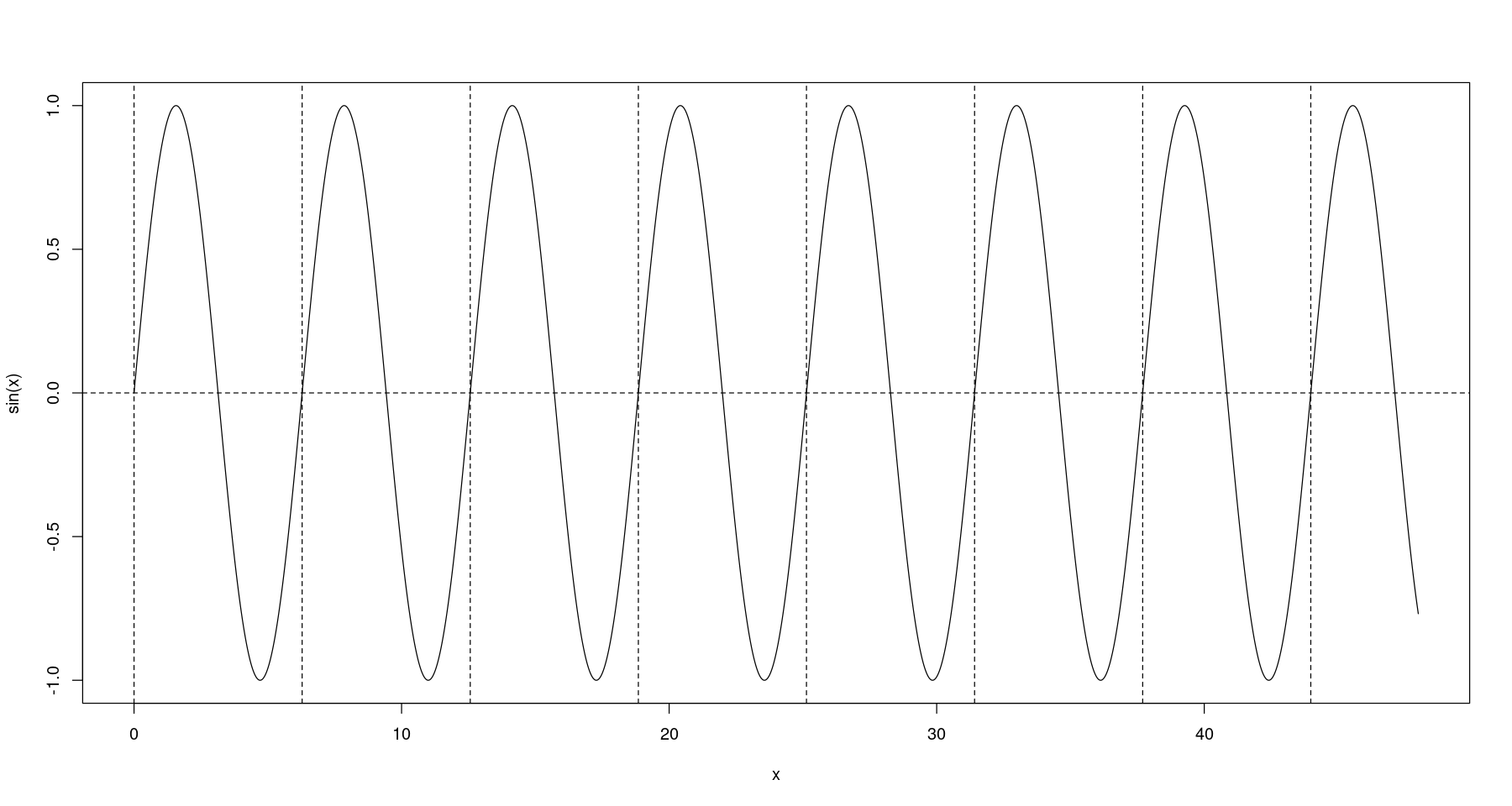

- \(cos(x)\): 주기가 2\(\pi\)인 주기 함수

plot(x, cos(x), type='l')
abline(h=0, lty=2)
abline(v=seq(0,48, by = 2*pi), lty=2)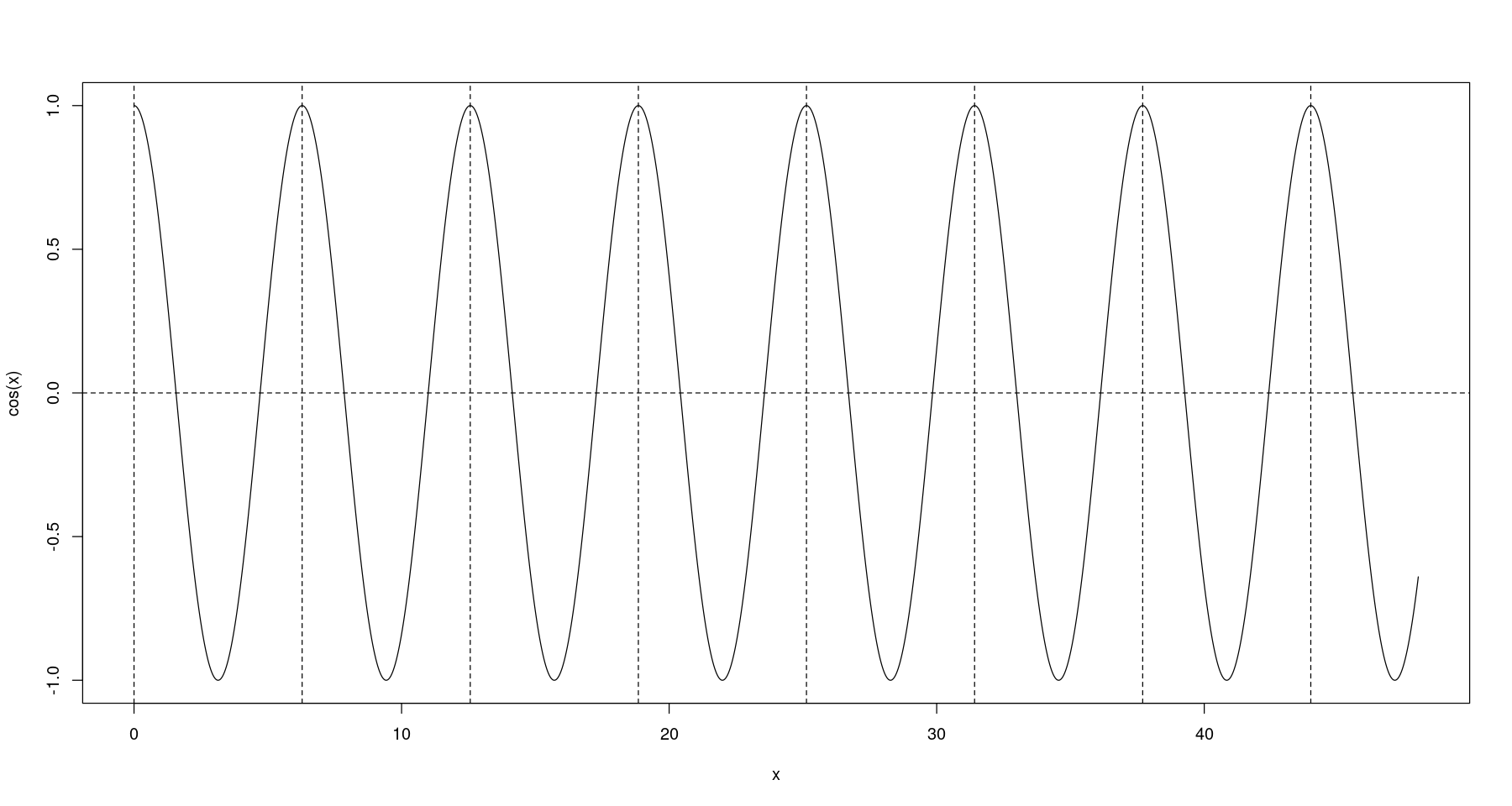

- 정리..

  • sin(x): 주기 2\(\pi\)
  • sin(2x): 주기 2\(\pi\)/2 = \(\pi\)
  • sin(3x): 주기 2\(\pi\)/3
  • sin(\(\pi\)x): 주기 2\(\pi\)/\(\pi\) = 2
  • sin(\(\pi\)x/6): 주기 12

주기를 s로 바꾸고 싶다면, s = 2 \(\pi\) / x => x = 2\(\pi\)s

- sin 함수의 주기 변동

# 주기 = pi
plot(x, sin(2*x), type='l', col='steelblue', lwd=2,
 xlab="", ylab="")
abline(h=0, lty=2)
abline(v= seq(0, 48, by=pi), lty=2)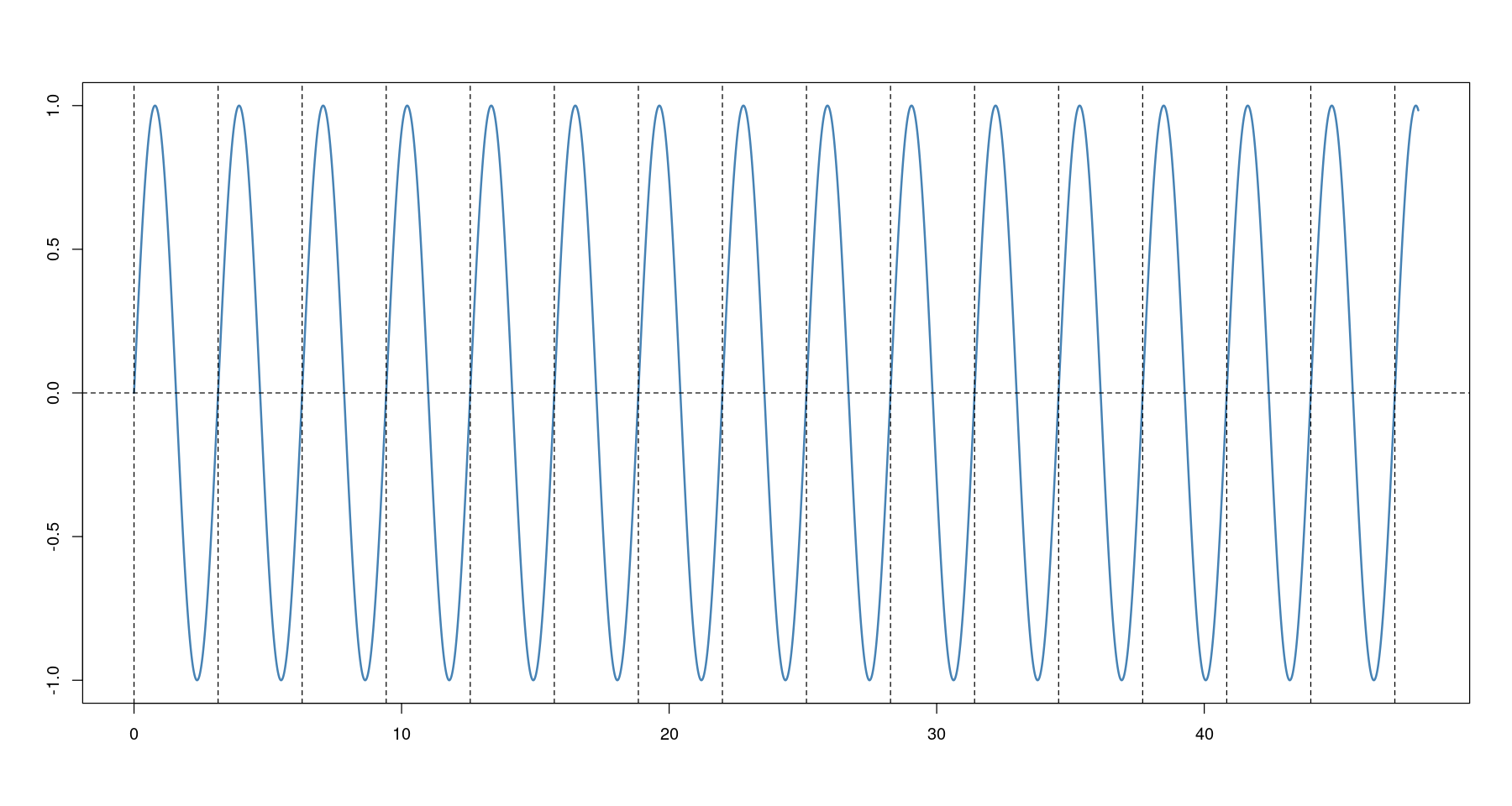

# 주기 = 12
s <- 12
plot(x, sin(2*pi*x/s), type='l', col='steelblue', lwd=2,
 xlab="", ylab="")
abline(h=0, lty=2)
abline(v= seq(0, 48, by=s), lty=2)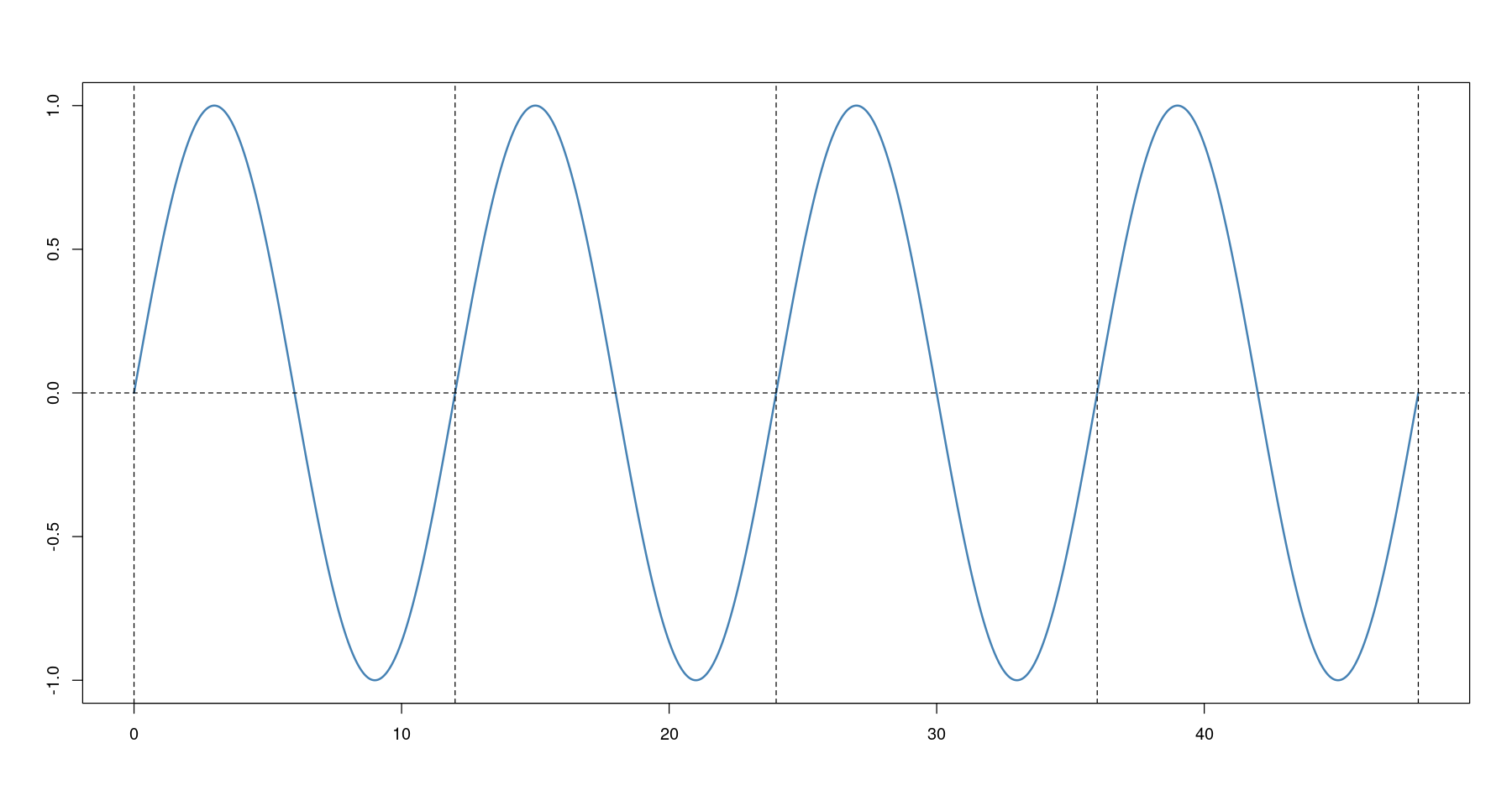

# 주기 = 4
s <- 4
plot(x, sin(2*pi*x/s), type='l', col='steelblue', lwd=2,
 xlab="", ylab="")
abline(h=0, lty=2)
abline(v= seq(0, 48, by=s), lty=2)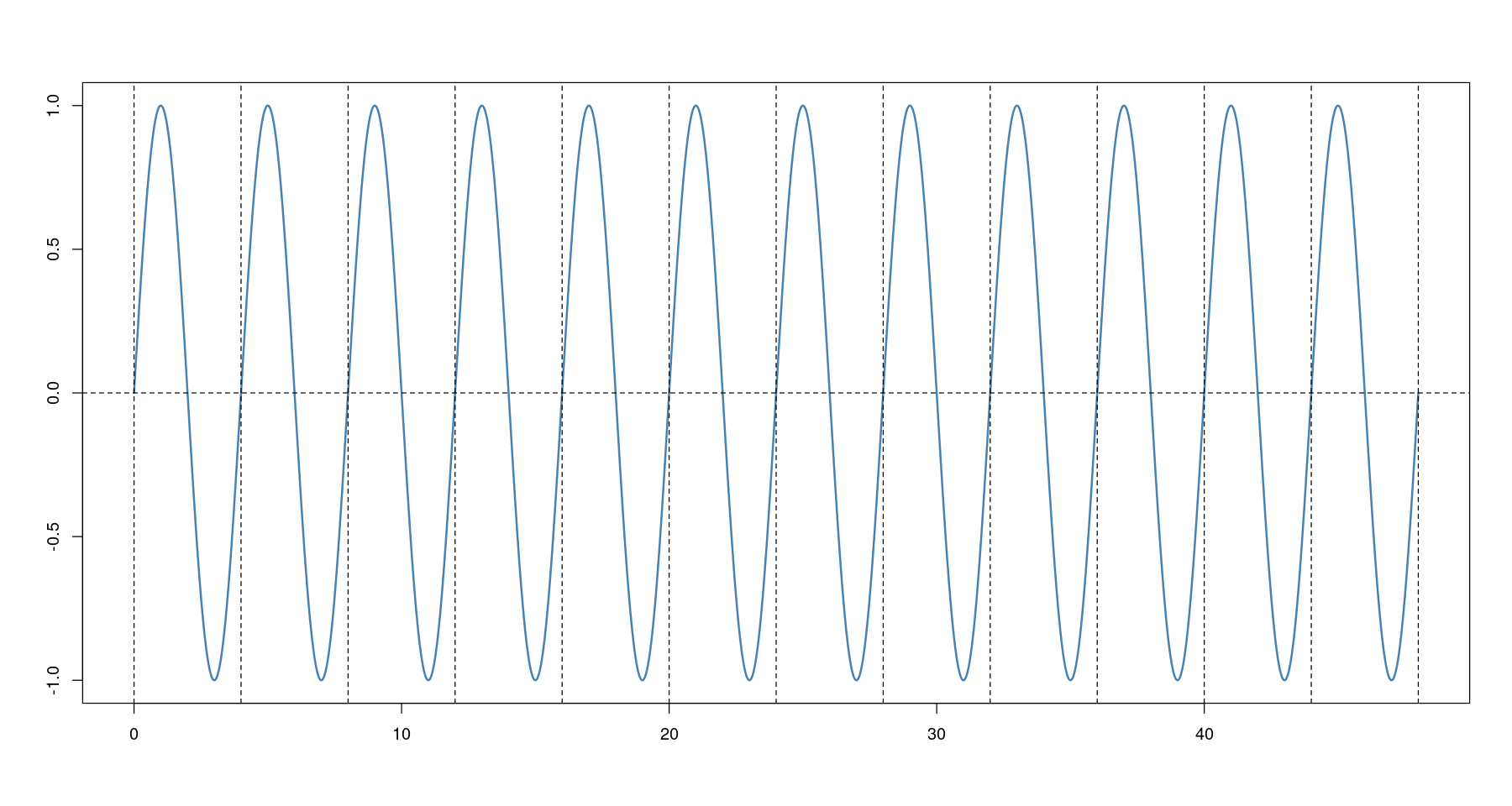

- sin + cos

s <- 12
plot(x, sin(2*pi*x/s)+cos(2*pi*x/s), type='l', col='steelblue', lwd=2,
 xlab="", ylab="", main=paste0('sin+cos :: ', "frequency=", s))
lines(x, sin(2*pi*x/s), col='grey1', lty=2)
lines(x, cos(2*pi*x/s), col='skyblue', lty=2)
abline(h=0, lty=2)
#abline(v= seq(0, 48, by=s), lty=2)
#abline(v= seq(1.5, 48, by=s), lty=2)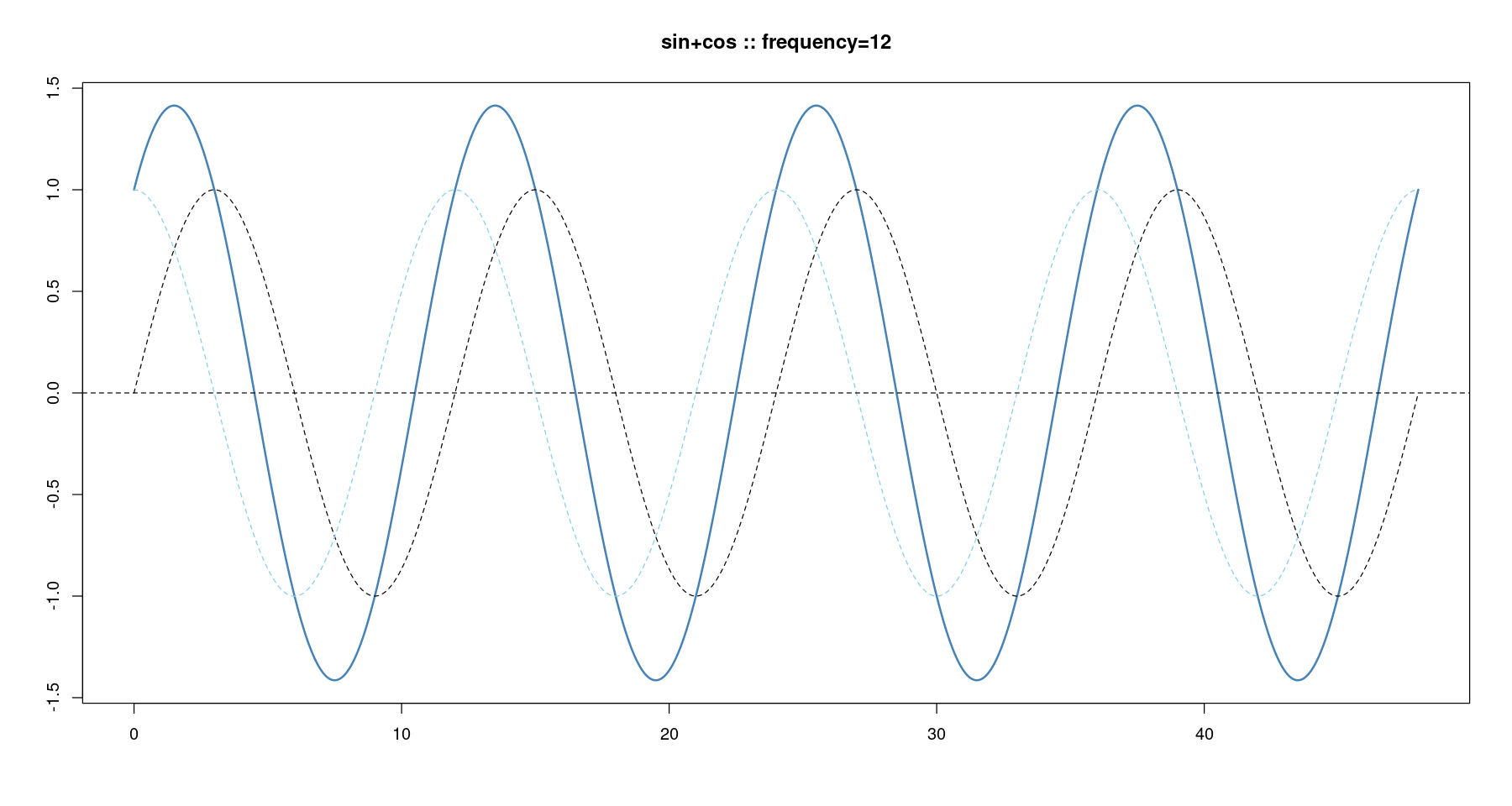

- 여러 주기의 함수 합치기

  • 주기가 12, 6인 sin함수 더하기: sin\(\left(\dfrac{2 \pi t}{12} \right)\) + sin\(\left(\dfrac{2 \pi t}{6} \right)\)
par(mfrow=c(3,1))
s<-12
plot(x, sin(2*pi*x/s), type='l', col='steelblue', lwd=2,
 xlab="", ylab="", main=paste0('sin :: ', "frequency=", s))
abline(h=0, lty=2)
abline(v= seq(0, 48, by=s), lty=2)
s<-6
plot(x, sin(2*pi*x/s), type='l', col='steelblue', lwd=2,
 xlab="", ylab="", main=paste0('sin :: ', "frequency=", s))
abline(h=0, lty=2)
abline(v= seq(0, 48, by=s), lty=2)
plot(x, sin(2*pi*x/12)+sin(2*pi*x/6), type='l', col='steelblue', lwd=2,
 xlab="", ylab="", main=paste0('sin :: ', "frequency=", s))
abline(h=0, lty=2)
abline(v= seq(0, 48, by=12), lty=2)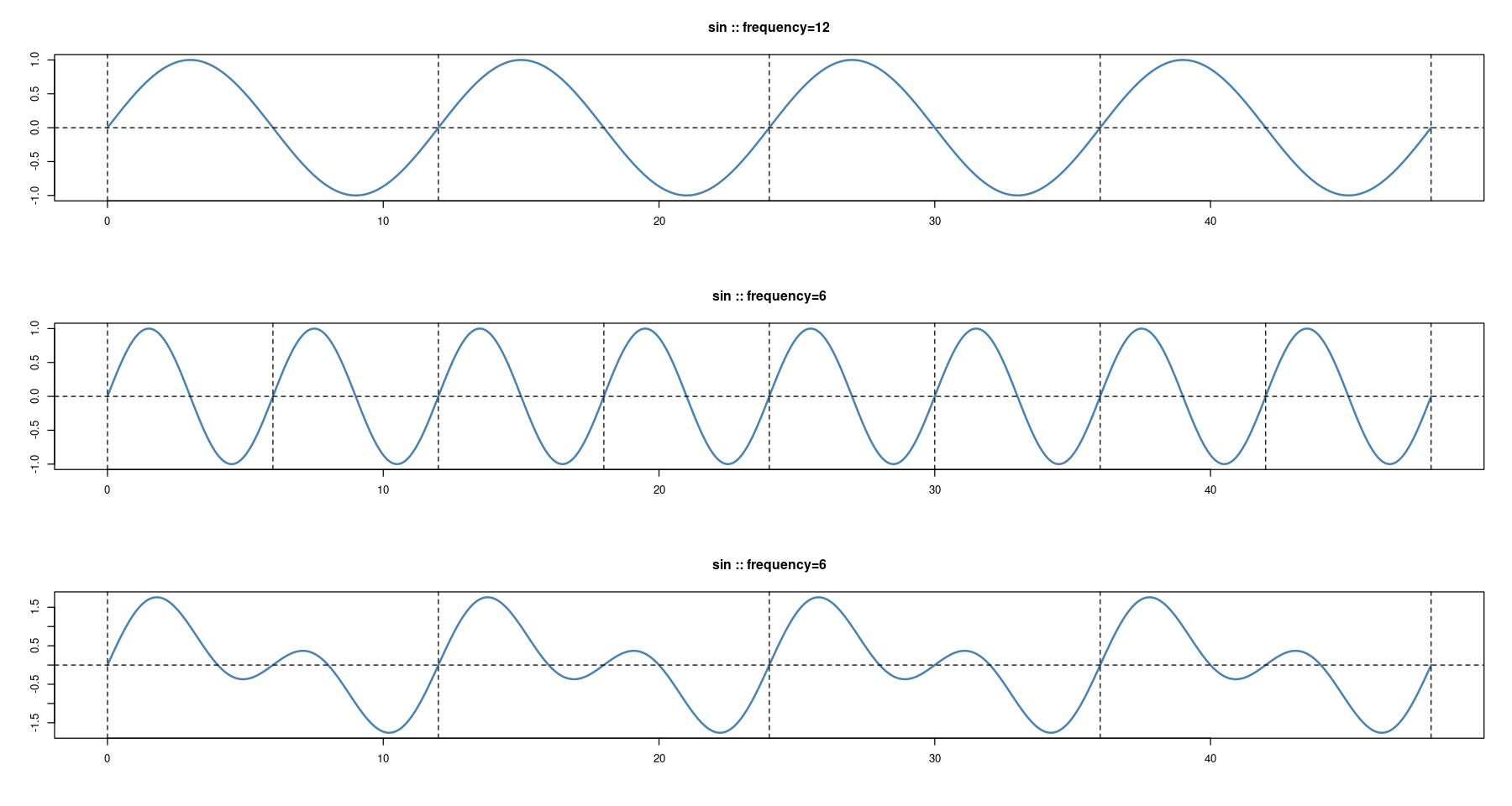

  • 주기가 12, 6인 sin함수 더하기: \(2sin \left(\dfrac{2 \pi t}{12} \right)\) + \(0.8sin\left(\dfrac{2 \pi t}{6} \right)\)
plot(x, 2*sin(2*pi*x/12)+0.8*sin(2*pi*x/6), type='l', col='steelblue', lwd=2,
 xlab="", ylab="", main=paste0('sin :: ', "frequency=", s),cex.main=2)
abline(h=0, lty=2)
abline(v= seq(0, 48, by=12), lty=2)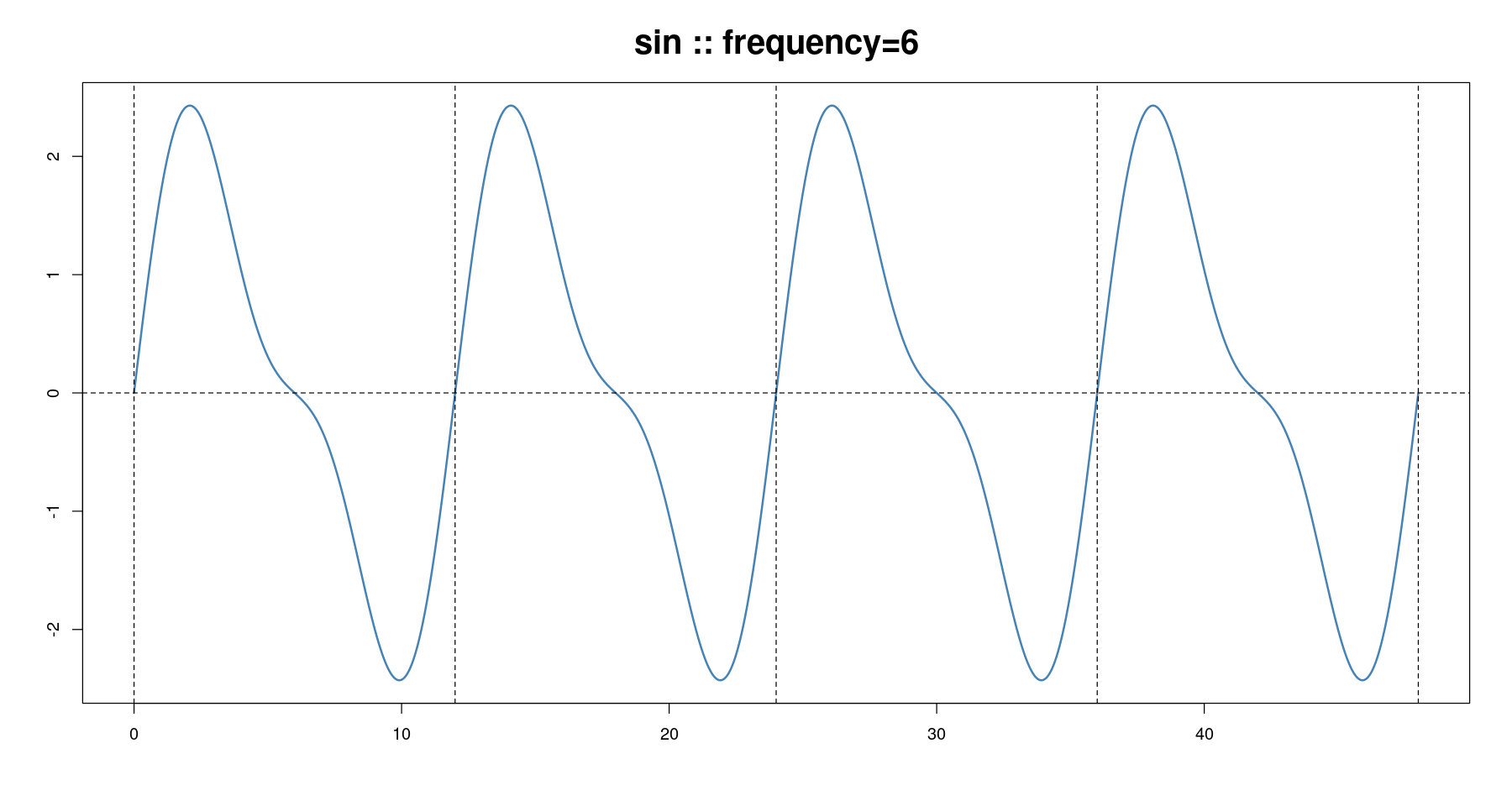

  • 주기가 12, 6, 3인 sin함수 더하기: \(sin \left(\dfrac{2 \pi t}{12} \right)\) + \(sin\left(\dfrac{2 \pi t}{6} \right)\) + \(sin\left(\dfrac{2 \pi t}{3} \right)\)
par(mfrow=c(3,1))
s<-12
plot(x, sin(2*pi*x/s), type='l', col='steelblue', lwd=2,
 xlab="", ylab="", main=paste0('sin :: ', "frequency=", s),cex.main=2)
abline(h=0, lty=2)
abline(v= seq(0, 24, by=s), lty=2)
s<-6
plot(x, sin(2*pi*x/s), type='l', col='steelblue', lwd=2,
 xlab="", ylab="", main=paste0('sin :: ', "frequency=", s),cex.main=2)
abline(h=0, lty=2)
abline(v= seq(0, 24, by=s), lty=2)
s<-3
plot(x, sin(2*pi*x/s), type='l', col='steelblue', lwd=2,
 xlab="", ylab="", main=paste0('sin :: ', "frequency=", s),cex.main=2)
abline(h=0, lty=2)
abline(v= seq(0, 24, by=s), lty=2)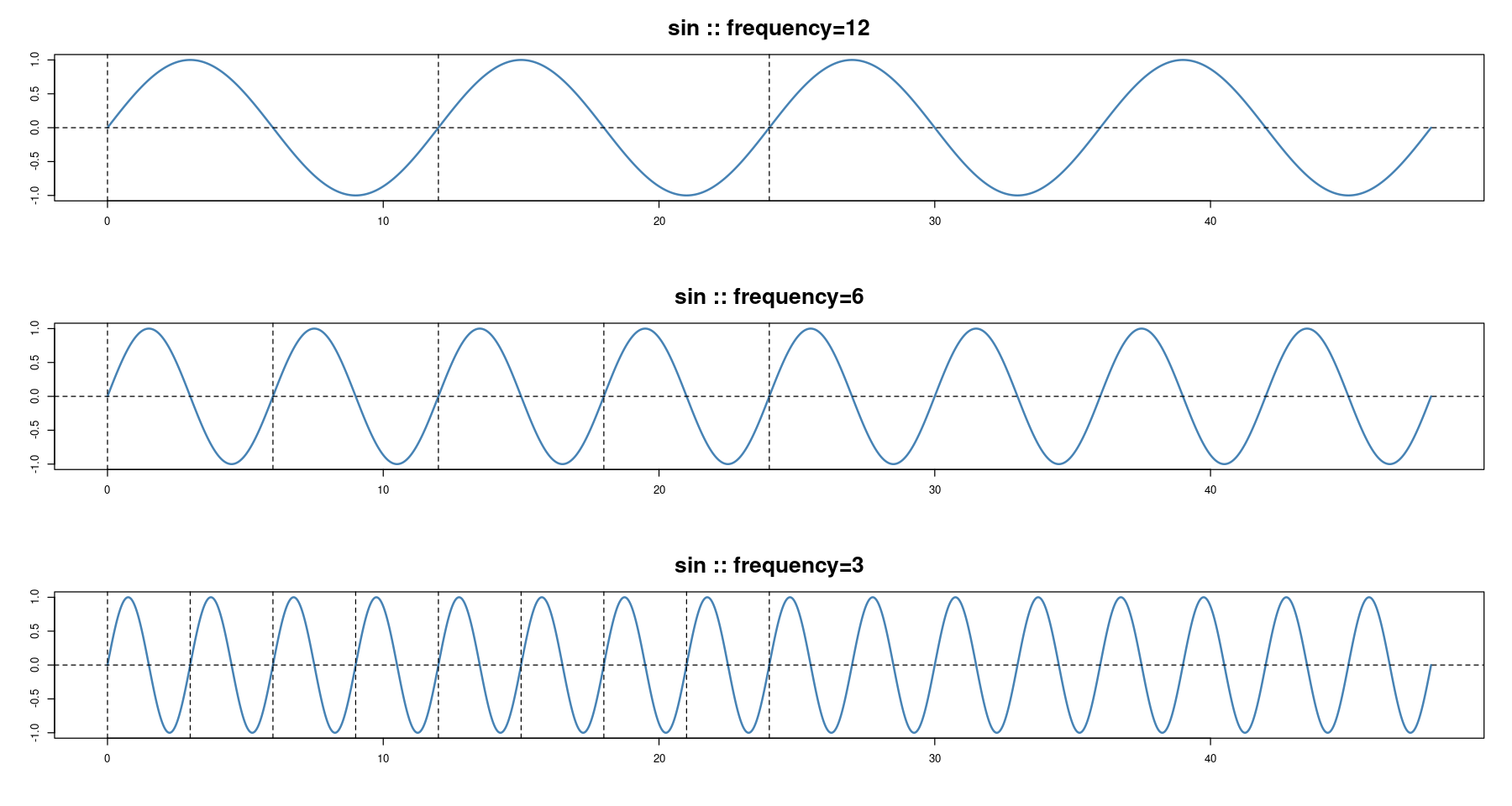

plot(x, sin(2*pi*x/12)+sin(2*pi*x/6)+sin(2*pi*x/3), type='l', col='steelblue', lwd=2,
 xlab="", ylab="", main=paste0('sin + sin + sin :: ', "frequency=", 12),cex.main=2)
abline(h=0, lty=2)
abline(v= seq(0, 24, by=12), lty=2)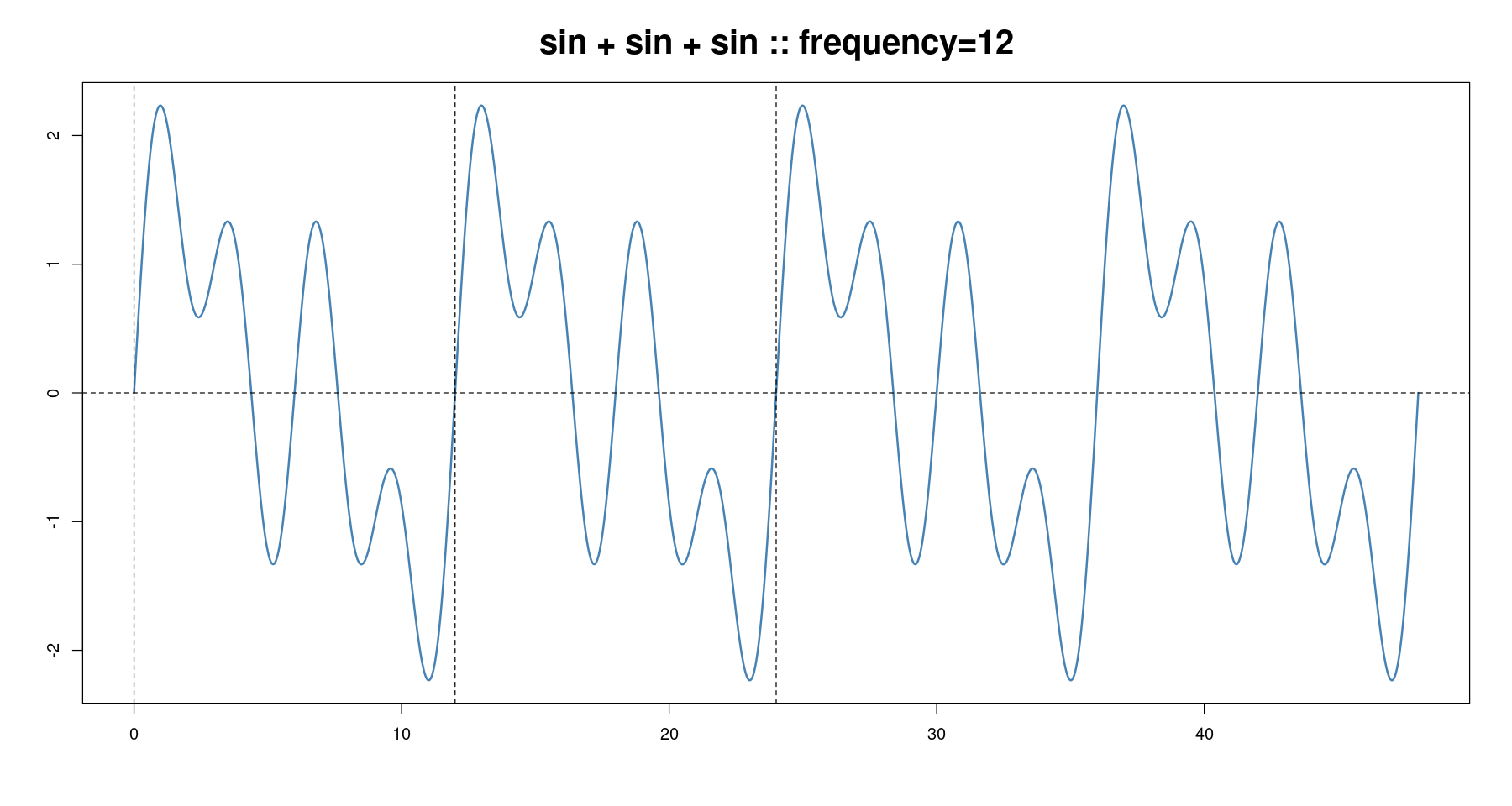

- 주기와 추세가 모두 있는 경우

par(mfrow=c(3,1))
plot(x, sin(2*pi*x/12)+sin(2*pi*x/6)+sin(2*pi*x/3),
     type='l', col='steelblue', lwd=2,
    xlab="", ylab="", main=paste0('sin + sin + sin :: ', "frequency=", 12), cex.main=2)
abline(h=0, lty=2)
abline(v= seq(0, 24, by=12), lty=2)

y <- sin(2*pi*x/12)+sin(2*pi*x/6)+sin(2*pi*x/3)+
    cos(2*pi*x/12)+cos(2*pi*x/6)+cos(2*pi*x/3)

plot(x,y, type='l', col='steelblue', lwd=2,
    xlab="", ylab="", main="s+s+s+c+c+c : frequency=12", cex.main=2)
abline(h=0, lty=2)
abline(v= seq(0, 24, by=12), lty=2)

y2 <- x*0.5 + sin(2*pi*x/12)+sin(2*pi*x/6)+sin(2*pi*x/3)+
    cos(2*pi*x/12)+cos(2*pi*x/6)+cos(2*pi*x/3)

plot(x,y2, type='l', col='steelblue', lwd=2,
    xlab="", ylab="", main="s+s+s+c+c+c : frequency=12", cex.main=2)
abline(a = 0, b = 0.5, lty=2)
abline(v= seq(0, 24, by=12), lty=2)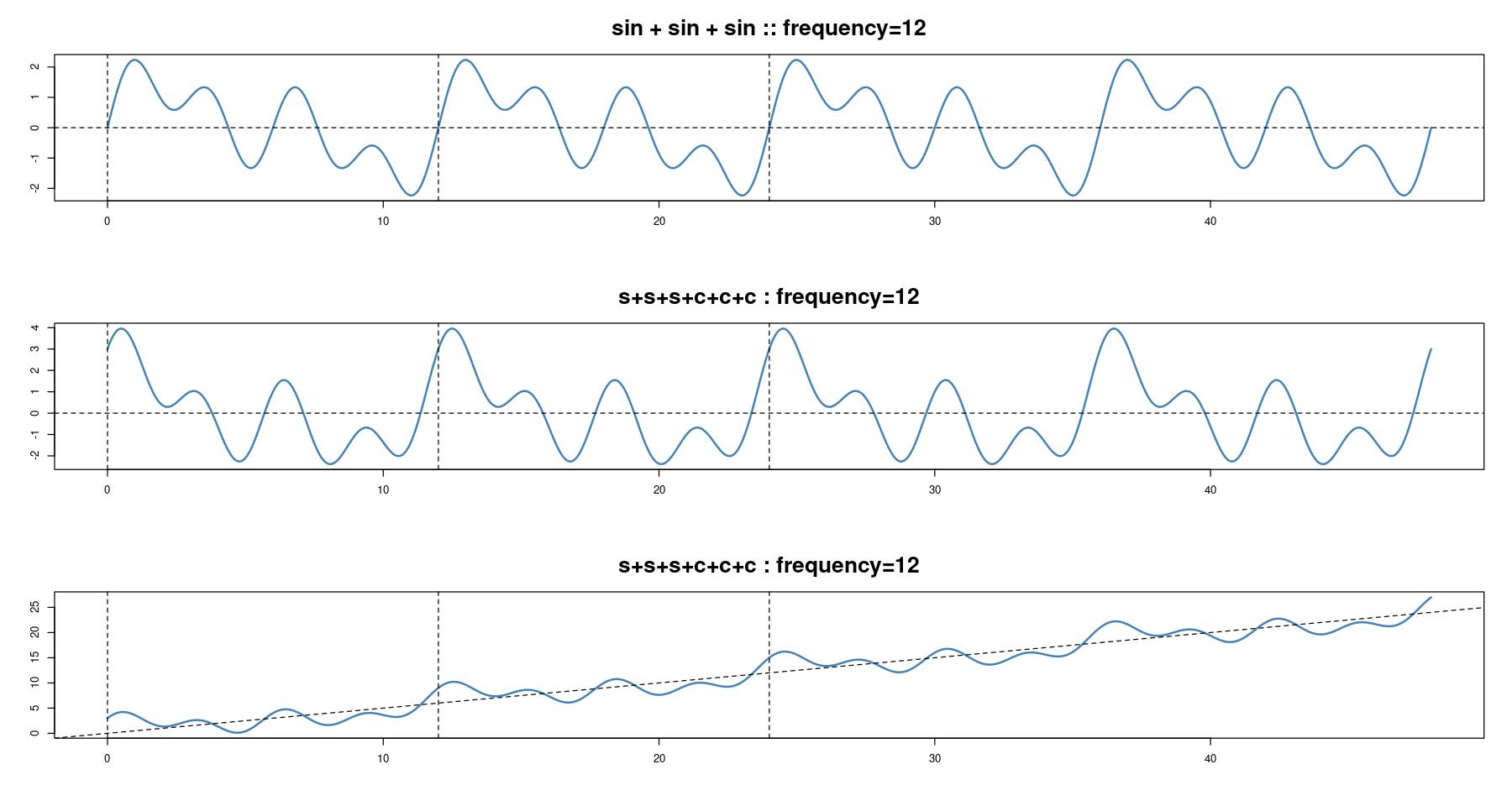

  • 강의노트에 있는 그림
n <- 100;
t <- 1:n
a1 <- -0.8;
a2 <- 1.4
phi1 <- pi/3;
phi2 <- 3*pi/4
first <- a1*sin(pi*t/6+phi1) # 첫 번째 주기성분
second <- a2*sin(pi*t/3+phi2) # 두 번째 주기성분

dt <- data.frame(t=t,
                 first = first,
                 second=second,
                 z = first+second)
p1 <- ggplot(dt, aes(t,first)) + geom_line(col='skyblue', size=1) +
 geom_point(col='steelblue', size=1)+
 ylim(-2.5,2)+xlab("")+
 scale_x_continuous(breaks = seq(1,100, by = 12))+
 theme_bw()

p2 <- ggplot(dt, aes(t,second)) + geom_line(col='skyblue', size=1) +
 geom_point(col='steelblue', size=1)+
 ylim(-2.5,2)+xlab("")+
 scale_x_continuous(breaks = seq(1,100, by = 12))+
 theme_bw()

p3 <- ggplot(dt, aes(t,z)) + geom_line(col='skyblue', size=1) +
 geom_point(col='steelblue', size=1)+
 scale_x_continuous(breaks = seq(1,100, by = 12))+
 ylim(-2.5,2)+xlab("")+
 theme_bw()

grid.arrange(p1, p2, p3, nrow = 3)
Warning message:
“Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
ℹ Please use `linewidth` instead.”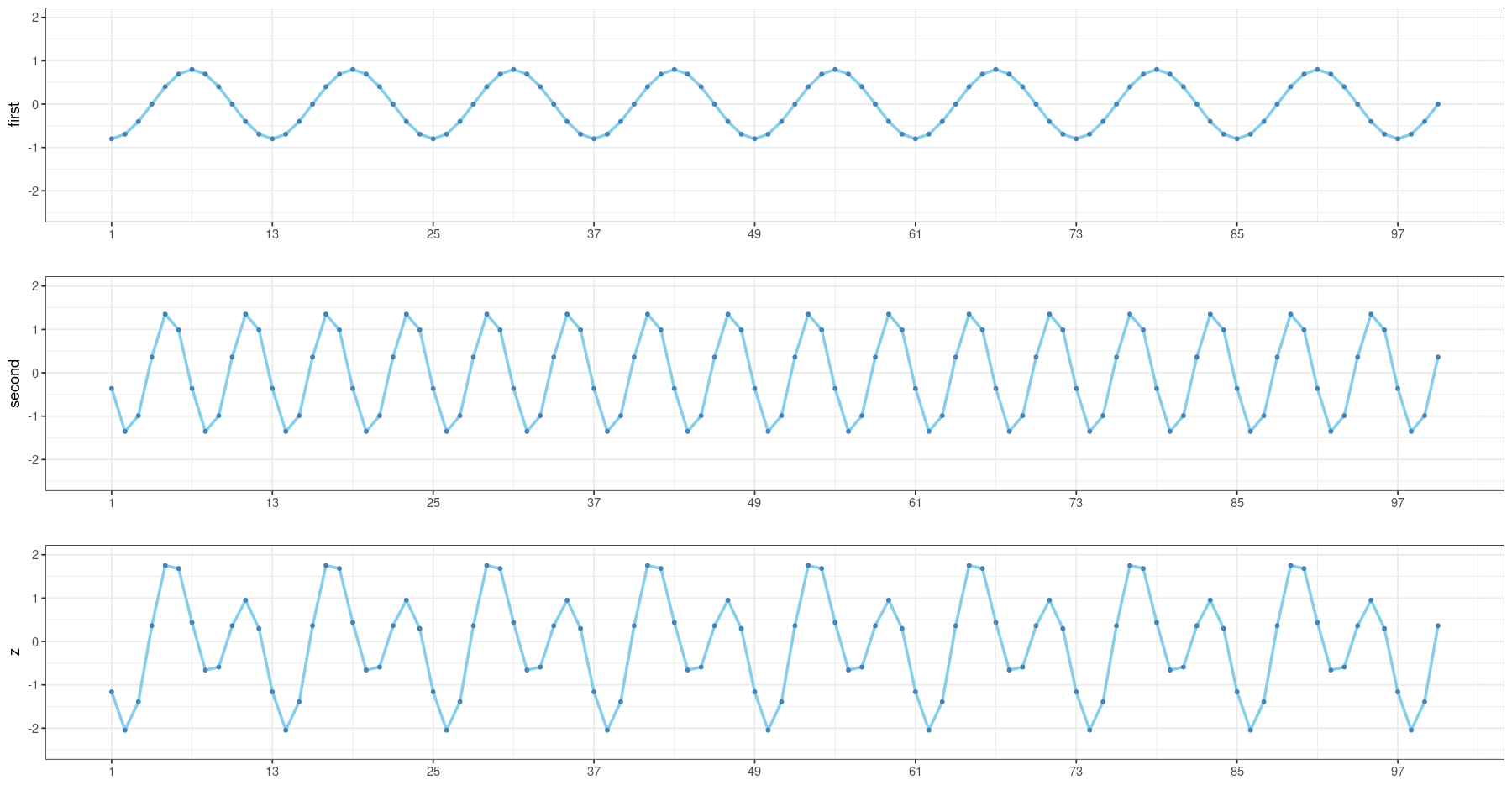

백화점 매출액 - 지시함수 사용

z <-scan("depart.txt")
head(z)
  1. 423
  2. 458
  3. 607
  4. 564
  5. 536
  6. 536
dep <- ts(z, frequency=12, start=c(1984,1))   # 1984년 1월부터 시작
plot(dep)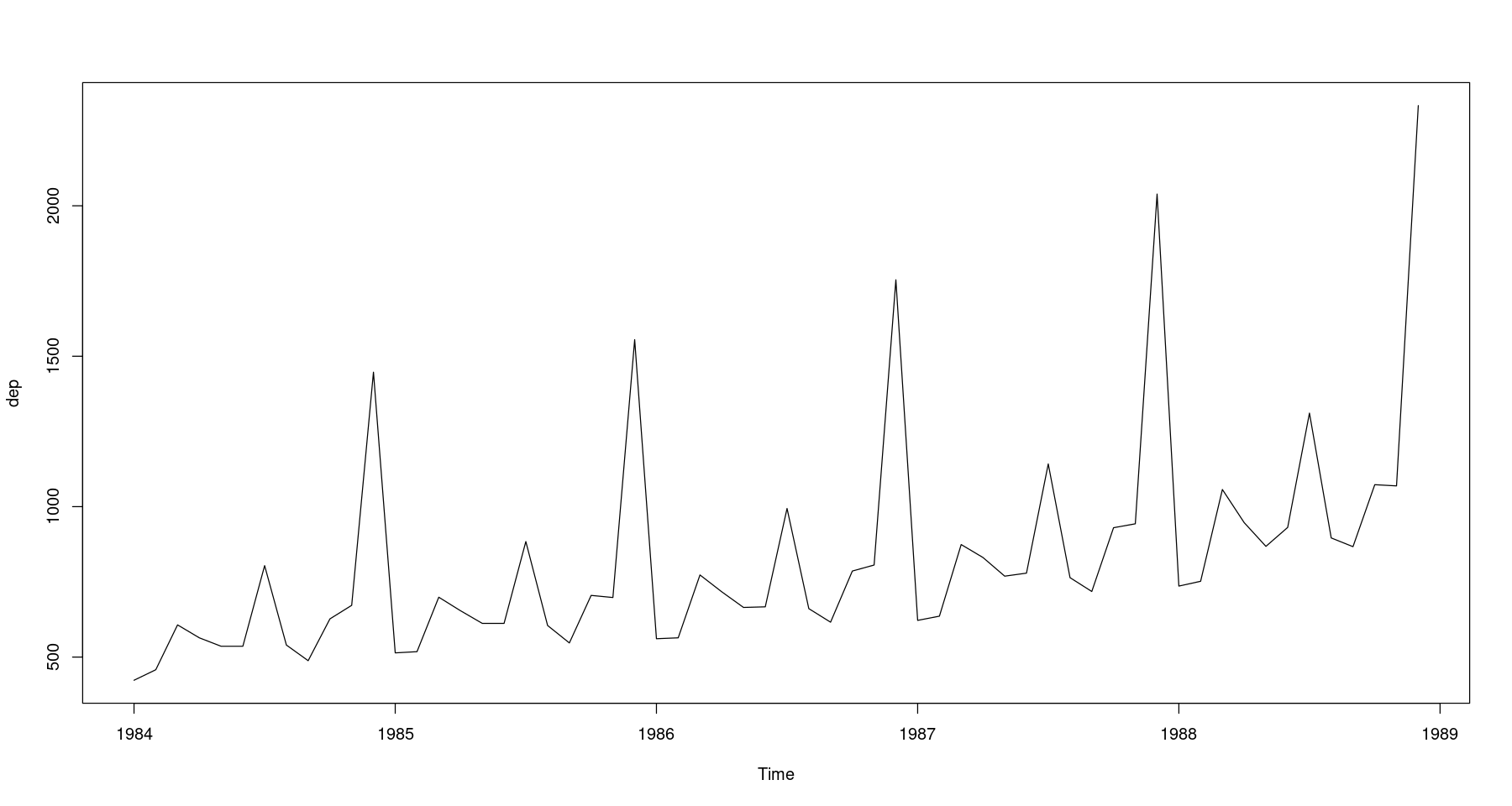

  • 약간 이분산성이 있어보인다. 로그변환이나 박스콕스변환을 하자.
class(dep)
'ts' 
cycle(dep)
A Time Series: 5 × 12
Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
1984 1 2 3 4 5 6 7 8 9 10 11 12
1985 1 2 3 4 5 6 7 8 9 10 11 12
1986 1 2 3 4 5 6 7 8 9 10 11 12
1987 1 2 3 4 5 6 7 8 9 10 11 12
1988 1 2 3 4 5 6 7 8 9 10 11 12

강의 영상..

lndep <- log(z)
plot(1:length(z), lndep, type='l')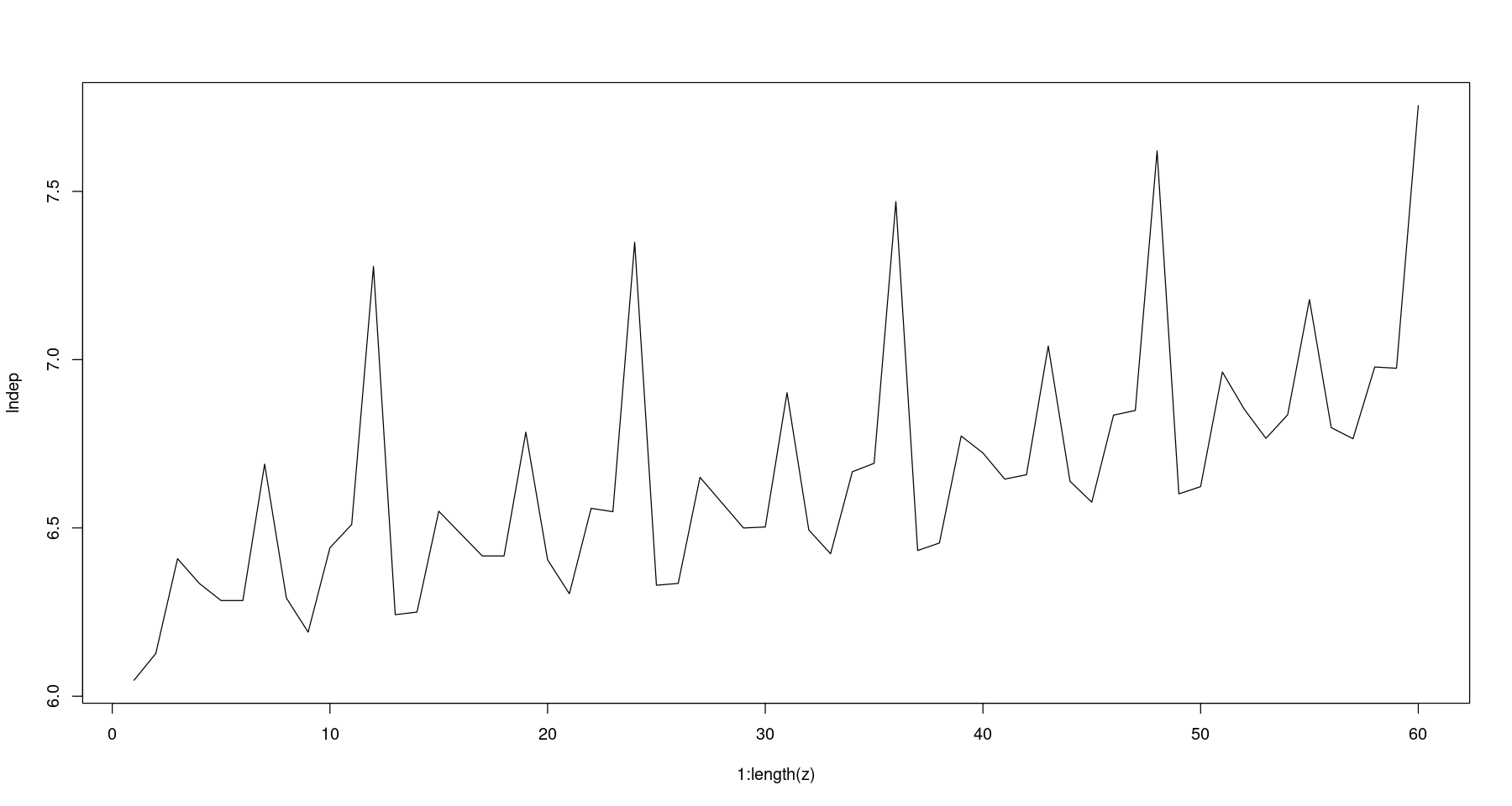

  • 등분산이 일정해 보인다.
trend <- 1:length(z)
trend    # 추세를 넣기 위해서 trend라는 변수 생성
  1. 1
  2. 2
  3. 3
  4. 4
  5. 5
  6. 6
  7. 7
  8. 8
  9. 9
  10. 10
  11. 11
  12. 12
  13. 13
  14. 14
  15. 15
  16. 16
  17. 17
  18. 18
  19. 19
  20. 20
  21. 21
  22. 22
  23. 23
  24. 24
  25. 25
  26. 26
  27. 27
  28. 28
  29. 29
  30. 30
  31. 31
  32. 32
  33. 33
  34. 34
  35. 35
  36. 36
  37. 37
  38. 38
  39. 39
  40. 40
  41. 41
  42. 42
  43. 43
  44. 44
  45. 45
  46. 46
  47. 47
  48. 48
  49. 49
  50. 50
  51. 51
  52. 52
  53. 53
  54. 54
  55. 55
  56. 56
  57. 57
  58. 58
  59. 59
  60. 60
reg <- lm(lndep ~ trend)
summary(reg)

Call:
lm(formula = lndep ~ trend)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.29916 -0.17726 -0.05602  0.04315  0.85621 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 6.271723   0.073109  85.786  < 2e-16 ***
trend       0.012443   0.002084   5.969 1.53e-07 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.2796 on 58 degrees of freedom
Multiple R-squared:  0.3806,    Adjusted R-squared:  0.3699 
F-statistic: 35.63 on 1 and 58 DF,  p-value: 1.531e-07
  • 1차 선형 모형
reg <- lm(lndep ~ trend + cycle(dep))   # 주기함수가 cycle이라 했으니, cycle을 넣어주면 될까 하고 넣어보자!
summary(reg)

Call:
lm(formula = lndep ~ trend + cycle(dep))

Residuals:
     Min       1Q   Median       3Q      Max 
-0.36677 -0.16421 -0.04285  0.12101  0.57652 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 6.034507   0.077684  77.680  < 2e-16 ***
trend       0.010660   0.001789   5.958 1.68e-07 ***
cycle(dep)  0.044858   0.008976   4.998 5.85e-06 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.2352 on 57 degrees of freedom
Multiple R-squared:  0.5693,    Adjusted R-squared:  0.5542 
F-statistic: 37.67 on 2 and 57 DF,  p-value: 3.754e-11

여기서 cycle은 1~12라는 수치형으로 넣어진 거라.. 범주형 변수로 바꿔줘야 한다.

reg <- lm(lndep ~ trend + as.factor(cycle(dep)))  
summary(reg)

Call:
lm(formula = lndep ~ trend + as.factor(cycle(dep)))

Residuals:
      Min        1Q    Median        3Q       Max 
-0.038679 -0.018689 -0.001468  0.015185  0.057288 

Coefficients:
                         Estimate Std. Error t value Pr(>|t|)    
(Intercept)             6.0641904  0.0122952 493.215  < 2e-16 ***
trend                   0.0106603  0.0001925  55.388  < 2e-16 ***
as.factor(cycle(dep))2  0.0166091  0.0160024   1.038   0.3046    
as.factor(cycle(dep))3  0.3169279  0.0160059  19.801  < 2e-16 ***
as.factor(cycle(dep))4  0.2311551  0.0160117  14.437  < 2e-16 ***
as.factor(cycle(dep))5  0.1490488  0.0160198   9.304 3.12e-12 ***
as.factor(cycle(dep))6  0.1555867  0.0160302   9.706 8.32e-13 ***
as.factor(cycle(dep))7  0.5243161  0.0160429  32.682  < 2e-16 ***
as.factor(cycle(dep))8  0.1200927  0.0160579   7.479 1.54e-09 ***
as.factor(cycle(dep))9  0.0359244  0.0160752   2.235   0.0302 *  
as.factor(cycle(dep))10 0.2692601  0.0160948  16.730  < 2e-16 ***
as.factor(cycle(dep))11 0.2775212  0.0161166  17.220  < 2e-16 ***
as.factor(cycle(dep))12 1.0462912  0.0161407  64.823  < 2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.0253 on 47 degrees of freedom
Multiple R-squared:  0.9959,    Adjusted R-squared:  0.9948 
F-statistic: 949.2 on 12 and 47 DF,  p-value: < 2.2e-16

근데 위에 좀 안이쁘니까 밑에 tmp.data라는 함수를 만들자.

tmp.data <- data.frame(
    dep = z,
    lndep = log(z),
    day = seq(ymd("1984-01-01"), by = "1 month", length.out = length(z)),
    s = as.factor(cycle(dep)),
    t = 1:length(z)
    )
head(tmp.data)
A data.frame: 6 × 5
dep lndep day s t
<dbl> <dbl> <date> <fct> <int>
1 423 6.047372 1984-01-01 1 1
2 458 6.126869 1984-02-01 2 2
3 607 6.408529 1984-03-01 3 3
4 564 6.335054 1984-04-01 4 4
5 536 6.284134 1984-05-01 5 5
6 536 6.284134 1984-06-01 6 6
  • 가변수를 넣을 때는 factor로!!
reg <- lm(lndep ~ t+s, tmp.data)      
summary(reg)

Call:
lm(formula = lndep ~ t + s, data = tmp.data)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.038679 -0.018689 -0.001468  0.015185  0.057288 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 6.0641904  0.0122952 493.215  < 2e-16 ***
t           0.0106603  0.0001925  55.388  < 2e-16 ***
s2          0.0166091  0.0160024   1.038   0.3046    
s3          0.3169279  0.0160059  19.801  < 2e-16 ***
s4          0.2311551  0.0160117  14.437  < 2e-16 ***
s5          0.1490488  0.0160198   9.304 3.12e-12 ***
s6          0.1555867  0.0160302   9.706 8.32e-13 ***
s7          0.5243161  0.0160429  32.682  < 2e-16 ***
s8          0.1200927  0.0160579   7.479 1.54e-09 ***
s9          0.0359244  0.0160752   2.235   0.0302 *  
s10         0.2692601  0.0160948  16.730  < 2e-16 ***
s11         0.2775212  0.0161166  17.220  < 2e-16 ***
s12         1.0462912  0.0161407  64.823  < 2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.0253 on 47 degrees of freedom
Multiple R-squared:  0.9959,    Adjusted R-squared:  0.9948 
F-statistic: 949.2 on 12 and 47 DF,  p-value: < 2.2e-16
  • 강의자료에서 있었던 제약조건을 생각하자.

beta0=0/beta1=0/sum_beta=0

위의 제약조건에서 아무런 내용이 없으면 beta1=0을 default로 설정함

  • 위의 summary 1월이 기준이므로

s2의 0.0166091 는 1월보다 이만큼 더 팔린다는 뜻이고..

s3의 0.3169279 는 1월보다 0.3만큼 더 팔린다는 뜻!

다른 것들은 거의 다 유의한데 s2는 별로 유의하지 않다. -> 왜? 1월과 2월의 시간차가 별로 없기 떄문에.. 1월보다 이만큼 더 팔리긴 하지만 통계적으로 더 유의하진 않아~ 라는 말.

reg2 <- lm(lndep ~ 0+t+s, tmp.data)  # 제약조건에서 beta0=0으로 놓는다는 뜻. 절편을 0으로!      
summary(reg2)

Call:
lm(formula = lndep ~ 0 + t + s, data = tmp.data)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.038679 -0.018689 -0.001468  0.015185  0.057288 

Coefficients:
     Estimate Std. Error t value Pr(>|t|)    
t   0.0106603  0.0001925   55.39   <2e-16 ***
s1  6.0641904  0.0122952  493.21   <2e-16 ***
s2  6.0807995  0.0123718  491.50   <2e-16 ***
s3  6.3811183  0.0124509  512.50   <2e-16 ***
s4  6.2953455  0.0125325  502.32   <2e-16 ***
s5  6.2132392  0.0126164  492.47   <2e-16 ***
s6  6.2197771  0.0127027  489.64   <2e-16 ***
s7  6.5885065  0.0127914  515.08   <2e-16 ***
s8  6.1842831  0.0128823  480.06   <2e-16 ***
s9  6.1001148  0.0129754  470.13   <2e-16 ***
s10 6.3334505  0.0130707  484.56   <2e-16 ***
s11 6.3417116  0.0131681  481.60   <2e-16 ***
s12 7.1104816  0.0132676  535.93   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.0253 on 47 degrees of freedom
Multiple R-squared:      1, Adjusted R-squared:      1 
F-statistic: 3.199e+05 on 13 and 47 DF,  p-value: < 2.2e-16
  • intersept가 없어짐!

s1이 의미하는 것은 1월 판매량의 평균

s2가 의미하는 것은 2월 판매량의 평균

모형의 유의하냐는 0이냐 그걸로 하는거라서 다 유의하다 나옴!

위에랑 차이는 계수 해석 조심하기.

reg3 <- lm(lndep ~ t+s, tmp.data,
           contrast = list(s="contr.sum"))
summary(reg3)

Call:
lm(formula = lndep ~ t + s, data = tmp.data, contrasts = list(s = "contr.sum"))

Residuals:
      Min        1Q    Median        3Q       Max 
-0.038679 -0.018689 -0.001468  0.015185  0.057288 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)  6.3260849  0.0067177 941.703  < 2e-16 ***
t            0.0106603  0.0001925  55.388  < 2e-16 ***
s1          -0.2618944  0.0108845 -24.061  < 2e-16 ***
s2          -0.2452853  0.0108675 -22.571  < 2e-16 ***
s3           0.0550335  0.0108538   5.070 6.63e-06 ***
s4          -0.0307393  0.0108436  -2.835  0.00674 ** 
s5          -0.1128456  0.0108368 -10.413 8.53e-14 ***
s6          -0.1063078  0.0108334  -9.813 5.87e-13 ***
s7           0.2624217  0.0108334  24.223  < 2e-16 ***
s8          -0.1418018  0.0108368 -13.085  < 2e-16 ***
s9          -0.2259700  0.0108436 -20.839  < 2e-16 ***
s10          0.0073656  0.0108538   0.679  0.50071    
s11          0.0156268  0.0108675   1.438  0.15708    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.0253 on 47 degrees of freedom
Multiple R-squared:  0.9959,    Adjusted R-squared:  0.9948 
F-statistic: 949.2 on 12 and 47 DF,  p-value: < 2.2e-16

  • 위의 코드는 제약 조건 중에 sum_beta=0인것을 의미함

  • 엇? s12가 없다! s12 = -(s1+ … + s11) 로 해석하면 됨

head(data.frame(hat_y1 = fitted(reg),
                hat_y2 = fitted(reg2),
                hat_y3 = fitted(reg3)))
A data.frame: 6 × 3
hat_y1 hat_y2 hat_y3
<dbl> <dbl> <dbl>
1 6.074851 6.074851 6.074851
2 6.102120 6.102120 6.102120
3 6.413099 6.413099 6.413099
4 6.337987 6.337987 6.337987
5 6.266541 6.266541 6.266541
6 6.283739 6.283739 6.283739

어떤 제약조건을 써도 fitted의 값은 똑같다! 계수 설명만 다름

plot(lndep ~ day, tmp.data, type='l')
lines(tmp.data$day, fitted(reg), col='darkorange', lty=2, lwd=2)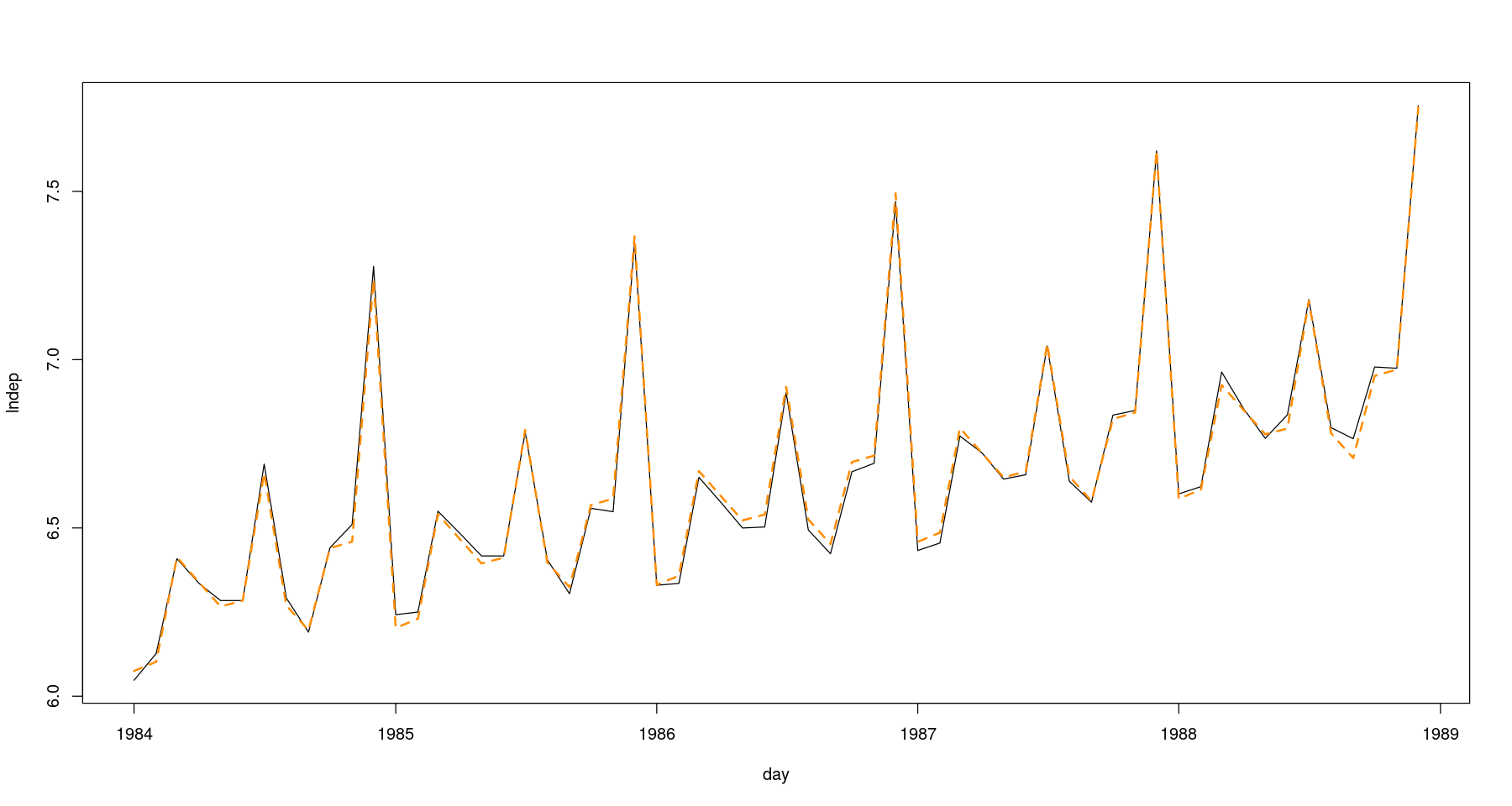

  • 실제값과 fittied value가 유사하게 가는 걸 확인할 수 있다.

강의 자료

tmp.data <- data.frame(
 day = seq(ymd("1984-01-01"),
 by='1 month', length.out=length(z)),
 z=z
)
head(tmp.data)
A data.frame: 6 × 2
day z
<date> <dbl>
1 1984-01-01 423
2 1984-02-01 458
3 1984-03-01 607
4 1984-04-01 564
5 1984-05-01 536
6 1984-06-01 536 
tmp.data$lndep <- log(z) #로그변환
tmp.data$y <- as.factor(as.integer(cycle(dep))) #지시함수로 사용할 주기
tmp.data$trend <- 1:length(z) #시간 변수 생성
head(tmp.data)
A data.frame: 6 × 5
day z lndep y trend
<date> <dbl> <dbl> <fct> <int>
1 1984-01-01 423 6.047372 1 1
2 1984-02-01 458 6.126869 2 2
3 1984-03-01 607 6.408529 3 3
4 1984-04-01 564 6.335054 4 4
5 1984-05-01 536 6.284134 5 5
6 1984-06-01 536 6.284134 6 6 
p1 <- ggplot(tmp.data, aes(day, z)) +
 geom_line(col='skyblue', lwd=2) +
 geom_point(col='steelblue', cex=1.5)+
 scale_x_date(date_breaks = "1 year", date_labels = "%Y-%m") +
 ggtitle("백화점 월별 매출액의 시계열그림") +
 theme_bw()+
 theme(axis.text = element_text(size =12),
       axis.title = element_blank(),
       title = element_text(size = 15))

p2 <- ggplot(tmp.data, aes(day, lndep)) +
 geom_line(col='skyblue', lwd=2) +
 geom_point(col='steelblue', cex=1.5)+
 scale_x_date(date_breaks = "1 year", date_labels = "%Y-%m") +
 ggtitle("로그변환 후 백화점 월별 매출액의 시계열그림") +
 theme_bw()+
 theme(axis.text = element_text(size =12),
       axis.title=element_blank(),
       title = element_text(size = 15))

grid.arrange(p1,p2,nrow=2)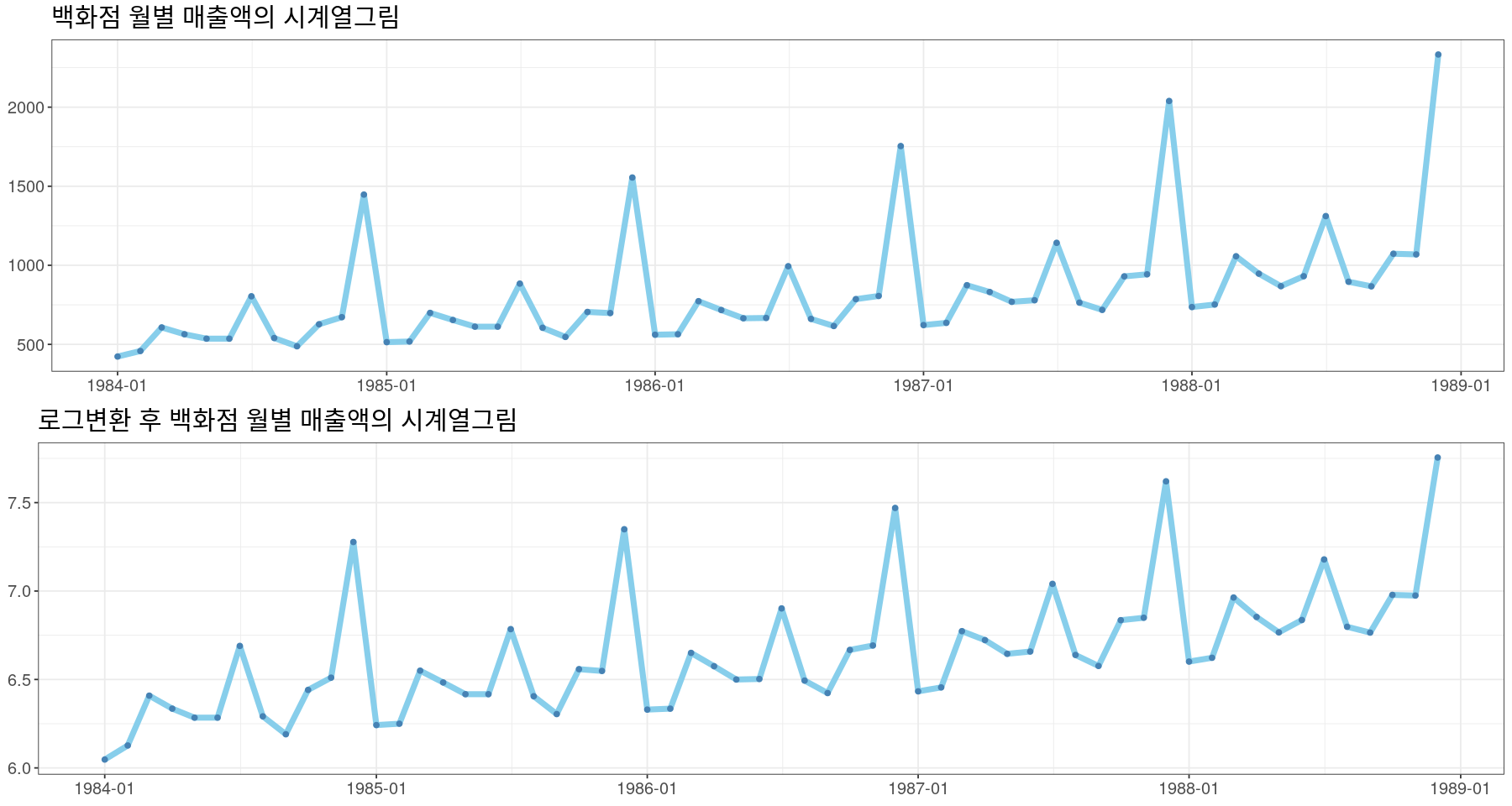

par(mfrow=c(2,1)) 
plot(z~day, tmp.data, type='l')
plot(log(z)~day, tmp.data, type='l')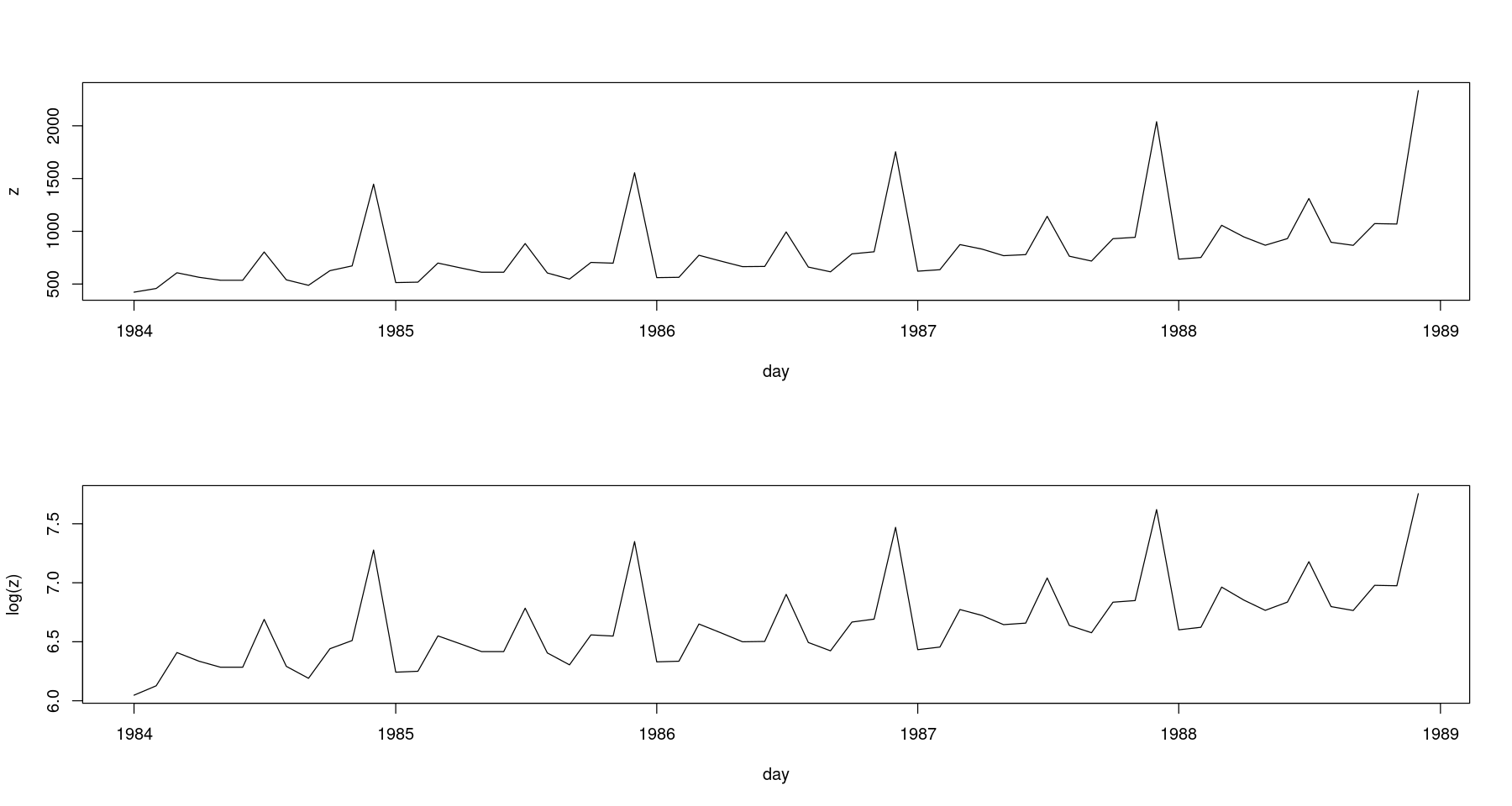

- 모형 적합: \(log(Z_t) = \beta_{trend}t + \beta_1 I_{t,1} + \dots + \beta_{12} I_{t,12} + \epsilon_t (\beta_0=0)\)

reg <- lm(lndep ~ 0 + trend+y, data=tmp.data ) #beta_0 = 0
summary(reg)

Call:
lm(formula = lndep ~ 0 + trend + y, data = tmp.data)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.038679 -0.018689 -0.001468  0.015185  0.057288 

Coefficients:
       Estimate Std. Error t value Pr(>|t|)    
trend 0.0106603  0.0001925   55.39   <2e-16 ***
y1    6.0641904  0.0122952  493.21   <2e-16 ***
y2    6.0807995  0.0123718  491.50   <2e-16 ***
y3    6.3811183  0.0124509  512.50   <2e-16 ***
y4    6.2953455  0.0125325  502.32   <2e-16 ***
y5    6.2132392  0.0126164  492.47   <2e-16 ***
y6    6.2197771  0.0127027  489.64   <2e-16 ***
y7    6.5885065  0.0127914  515.08   <2e-16 ***
y8    6.1842831  0.0128823  480.06   <2e-16 ***
y9    6.1001148  0.0129754  470.13   <2e-16 ***
y10   6.3334505  0.0130707  484.56   <2e-16 ***
y11   6.3417116  0.0131681  481.60   <2e-16 ***
y12   7.1104816  0.0132676  535.93   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.0253 on 47 degrees of freedom
Multiple R-squared:      1, Adjusted R-squared:      1 
F-statistic: 3.199e+05 on 13 and 47 DF,  p-value: < 2.2e-16

- 모형 적합: \(log(Z_t) = \beta_0+ \beta_{trend}t + \beta_2 I_{t,2} + \dots + \beta_{12} I_{t,12} + \epsilon_t (\beta_1=0)\)

reg2 <- lm(lndep ~ trend+y, data=tmp.data ) #beta_1=0
summary(reg2)

Call:
lm(formula = lndep ~ trend + y, data = tmp.data)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.038679 -0.018689 -0.001468  0.015185  0.057288 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 6.0641904  0.0122952 493.215  < 2e-16 ***
trend       0.0106603  0.0001925  55.388  < 2e-16 ***
y2          0.0166091  0.0160024   1.038   0.3046    
y3          0.3169279  0.0160059  19.801  < 2e-16 ***
y4          0.2311551  0.0160117  14.437  < 2e-16 ***
y5          0.1490488  0.0160198   9.304 3.12e-12 ***
y6          0.1555867  0.0160302   9.706 8.32e-13 ***
y7          0.5243161  0.0160429  32.682  < 2e-16 ***
y8          0.1200927  0.0160579   7.479 1.54e-09 ***
y9          0.0359244  0.0160752   2.235   0.0302 *  
y10         0.2692601  0.0160948  16.730  < 2e-16 ***
y11         0.2775212  0.0161166  17.220  < 2e-16 ***
y12         1.0462912  0.0161407  64.823  < 2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.0253 on 47 degrees of freedom
Multiple R-squared:  0.9959,    Adjusted R-squared:  0.9948 
F-statistic: 949.2 on 12 and 47 DF,  p-value: < 2.2e-16
contrasts(tmp.data$y)
A matrix: 12 × 11 of type dbl
2 3 4 5 6 7 8 9 10 11 12
1 0 0 0 0 0 0 0 0 0 0 0
2 1 0 0 0 0 0 0 0 0 0 0
3 0 1 0 0 0 0 0 0 0 0 0
4 0 0 1 0 0 0 0 0 0 0 0
5 0 0 0 1 0 0 0 0 0 0 0
6 0 0 0 0 1 0 0 0 0 0 0
7 0 0 0 0 0 1 0 0 0 0 0
8 0 0 0 0 0 0 1 0 0 0 0
9 0 0 0 0 0 0 0 1 0 0 0
10 0 0 0 0 0 0 0 0 1 0 0
11 0 0 0 0 0 0 0 0 0 1 0
12 0 0 0 0 0 0 0 0 0 0 1

- 모형 적합: \(log(Z_t) = \beta_0+ \beta_{trend}t + \beta_1 I_{t,1} + \dots + \beta_{11} I_{t,11} + \epsilon_t (\sum_{i=1}^{12} \beta_i=0)\)

reg3 <- lm(lndep ~ trend+y, data=tmp.data,
 contrasts = list(y = "contr.sum")) #sum beta_i = 0
# b1 + ... +b12 = 0 => b12 = -(b1+...+b11)
summary(reg3)

Call:
lm(formula = lndep ~ trend + y, data = tmp.data, contrasts = list(y = "contr.sum"))

Residuals:
      Min        1Q    Median        3Q       Max 
-0.038679 -0.018689 -0.001468  0.015185  0.057288 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)  6.3260849  0.0067177 941.703  < 2e-16 ***
trend        0.0106603  0.0001925  55.388  < 2e-16 ***
y1          -0.2618944  0.0108845 -24.061  < 2e-16 ***
y2          -0.2452853  0.0108675 -22.571  < 2e-16 ***
y3           0.0550335  0.0108538   5.070 6.63e-06 ***
y4          -0.0307393  0.0108436  -2.835  0.00674 ** 
y5          -0.1128456  0.0108368 -10.413 8.53e-14 ***
y6          -0.1063078  0.0108334  -9.813 5.87e-13 ***
y7           0.2624217  0.0108334  24.223  < 2e-16 ***
y8          -0.1418018  0.0108368 -13.085  < 2e-16 ***
y9          -0.2259700  0.0108436 -20.839  < 2e-16 ***
y10          0.0073656  0.0108538   0.679  0.50071    
y11          0.0156268  0.0108675   1.438  0.15708    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.0253 on 47 degrees of freedom
Multiple R-squared:  0.9959,    Adjusted R-squared:  0.9948 
F-statistic: 949.2 on 12 and 47 DF,  p-value: < 2.2e-16
head(data.frame(hat_y1 = fitted(reg),
 hat_y2 = fitted(reg2),
 hat_y3 = fitted(reg3)))
A data.frame: 6 × 3
hat_y1 hat_y2 hat_y3
<dbl> <dbl> <dbl>
1 6.074851 6.074851 6.074851
2 6.102120 6.102120 6.102120
3 6.413099 6.413099 6.413099
4 6.337987 6.337987 6.337987
5 6.266541 6.266541 6.266541
6 6.283739 6.283739 6.283739 
plot(lndep~day, tmp.data,
 main = 'observation vs. fitted value',
 xlab="", ylab="",
 type='l',
 col='skyblue',
 lwd=2, cex.axis=2, cex.main=2) +
 points(lndep~day, tmp.data, col="steelblue", cex=2, pch=16) +
 lines(tmp.data$day, fitted(reg), col='red', lty=2, lwd=2)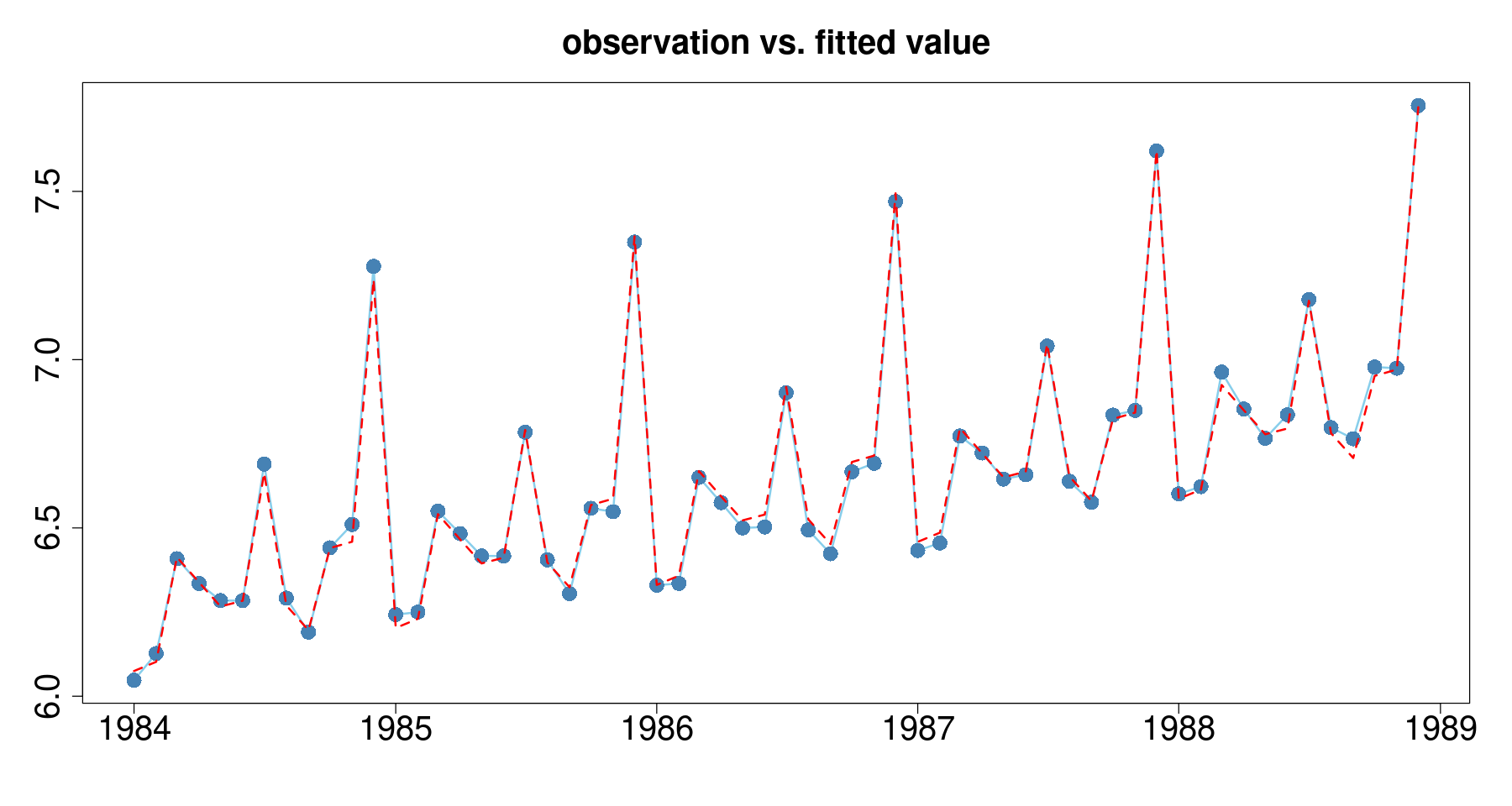

잔차 분석

plot(tmp.data$day, resid(reg),
 pch=16, cex=2, xaxt='n', type='b',
 xlab="", ylab="", main="잔차의 시계열 그림", cex.main=2)
abline(h=0, lty=2, lwd=2)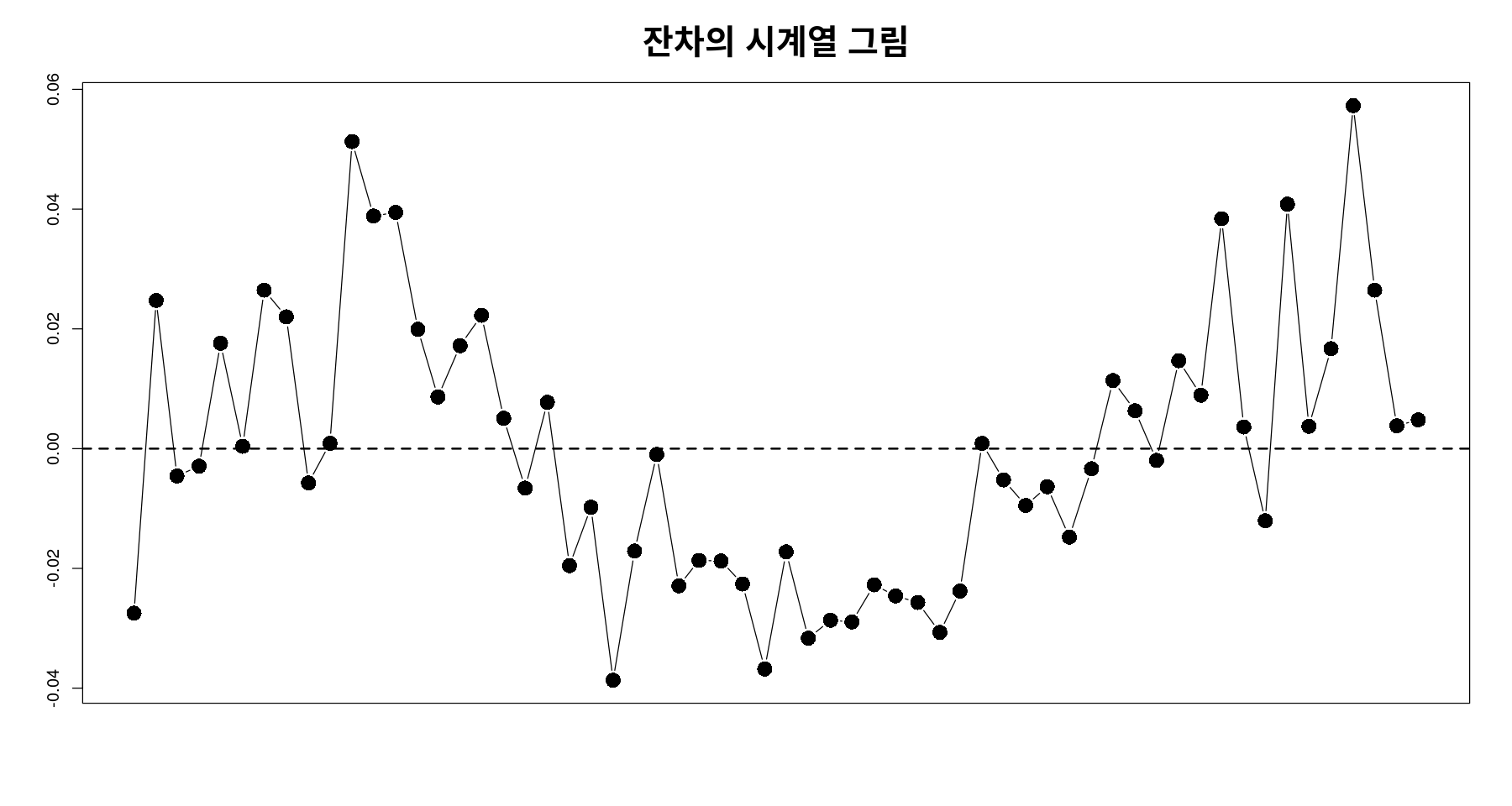

독립성 검정 : dW test

dwtest(reg, , alternative="two.sided")

    Durbin-Watson test

data:  reg
DW = 0.82642, p-value = 4.781e-06
alternative hypothesis: true autocorrelation is not 0

유의확률도 작고 기각할수 있고 양의 상관관계..

dwtest(reg)

    Durbin-Watson test

data:  reg
DW = 0.82642, p-value = 2.39e-06
alternative hypothesis: true autocorrelation is greater than 0

정규분포 검정 (shapiro-wilk test)

- 가설

\(H_0\): 정규분포를 따른다. VS \(H_1\): 정규분포를 따르지 않는다.

hist(resid(reg))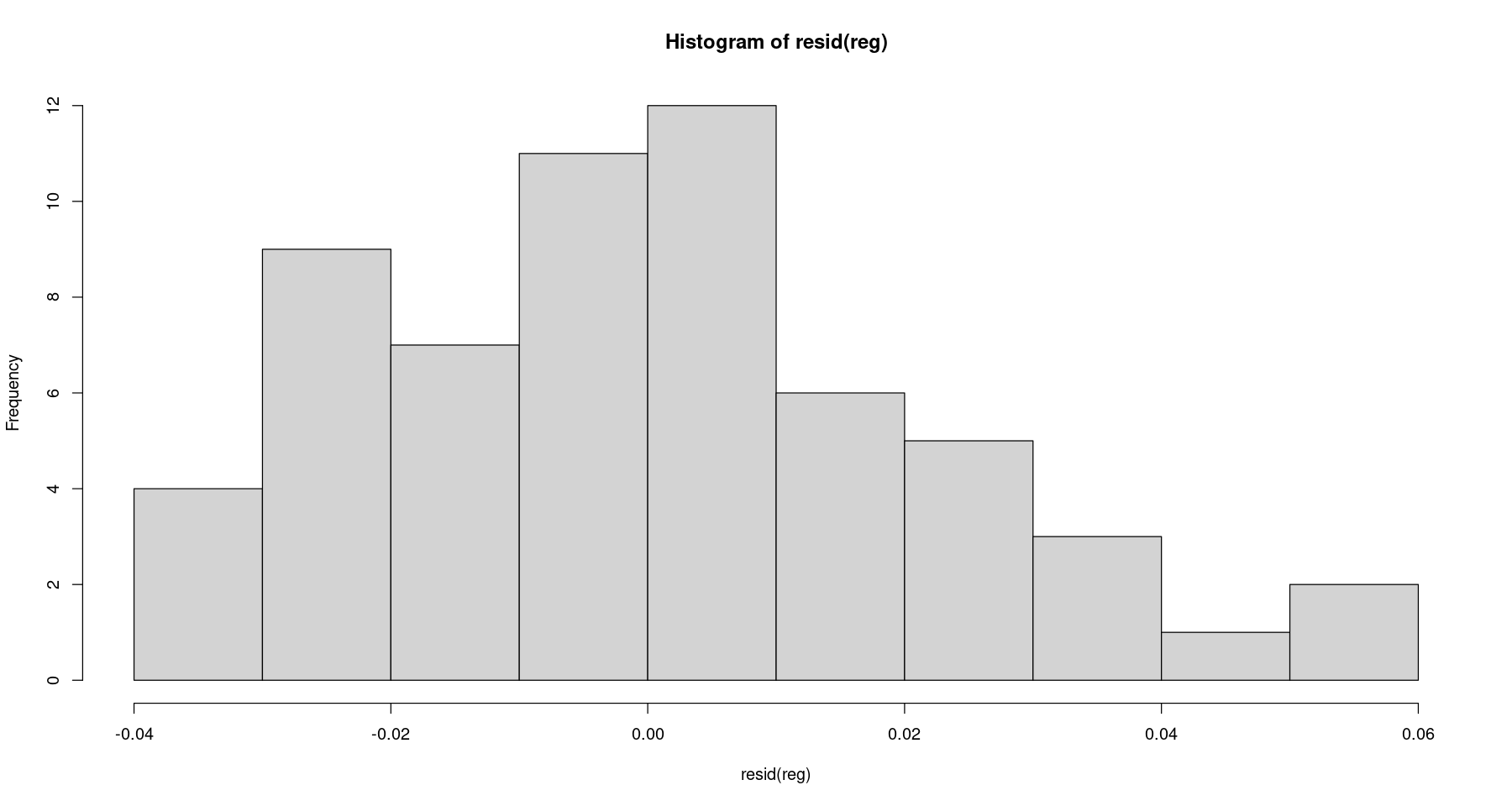

shapiro.test(resid(reg)) #H_0 : 정규분포를 따른다.

    Shapiro-Wilk normality test

data:  resid(reg)
W = 0.97114, p-value = 0.1659

정규분포를 따른다고 보자.

등분산성검정 (Breusch–Pagan test)

- 가설

\(H_0\): 등분산 VS \(H_1\): 이분산

bptest(reg)

    studentized Breusch-Pagan test

data:  reg
BP = 8.1109, df = 12, p-value = 0.7764

등분산성도 괜찮아 보인다.

적립값에 대한 MSE 구하기

\[MSE=\frac{1}{n} \sum_{t=1}^n (Z_t - \hat{Z_t})^2\]

오차항 제곱합에 대한 평균. 실제값과 평균값에 대하 차이를 n으로 나눈값

위에서 그림그릴때는 log값으로 했던 거니까, 실제로 실제 10년후? 20년후?를 생각할 때는 exp을 취해서 비교해주는게 원래 맞음

MSE! 그래서 밑에서 exp값 취해줌

mse1 = sum((tmp.data$dep - exp(fitted(reg)))^2)/60
mse1
353.669083494937 
hat_z = exp(fitted(reg))
head(hat_z)
1
434.784580002858
2
446.804031754714
3
609.780567125218
4
565.656296676459
5
526.652327873636
6
535.788096351339
mse_reg_indicator <- sum((z- hat_z)^2)/length(z)
mse_reg_indicator
353.669083494948

백화점 매출액 - 삼각함수 이용

- 데이터 생성

tmp.data_2 <- data.frame(
 lndep = tmp.data$lndep,
 trend = tmp.data$trend)
head(tmp.data_2)
A data.frame: 6 × 2
lndep trend
<dbl> <int>
1 6.047372 1
2 6.126869 2
3 6.408529 3
4 6.335054 4
5 6.284134 5
6 6.284134 6 
dt1 <- Reduce(cbind.data.frame, lapply(as.list(1:5), function(i) sin(2*pi*i/12*tmp.data_2$trend)))
head(dt1)
A data.frame: 6 × 5
init x[[i]] x[[i]] x[[i]] x[[i]]
<dbl> <dbl> <dbl> <dbl> <dbl>
1 5.000000e-01 8.660254e-01 1.000000e+00 8.660254e-01 5.000000e-01
2 8.660254e-01 8.660254e-01 1.224647e-16 -8.660254e-01 -8.660254e-01
3 1.000000e+00 1.224647e-16 -1.000000e+00 -2.449294e-16 1.000000e+00
4 8.660254e-01 -8.660254e-01 -2.449294e-16 8.660254e-01 -8.660254e-01
5 5.000000e-01 -8.660254e-01 1.000000e+00 -8.660254e-01 5.000000e-01
6 1.224647e-16 -2.449294e-16 3.673940e-16 -4.898587e-16 6.123234e-16

위 dataframe에서 init:사인 주기가 12인것. x[[i]]: 사인 주기가 6인거.. 주기 4 주기 3 주기 2.5? 인거까지 데이터 프레임이 들어감..

names(dt1) <- paste("sin", c(12,6,4,3,2.4), sep="_")
head(dt1)
A data.frame: 6 × 5
sin_12 sin_6 sin_4 sin_3 sin_2.4
<dbl> <dbl> <dbl> <dbl> <dbl>
1 5.000000e-01 8.660254e-01 1.000000e+00 8.660254e-01 5.000000e-01
2 8.660254e-01 8.660254e-01 1.224647e-16 -8.660254e-01 -8.660254e-01
3 1.000000e+00 1.224647e-16 -1.000000e+00 -2.449294e-16 1.000000e+00
4 8.660254e-01 -8.660254e-01 -2.449294e-16 8.660254e-01 -8.660254e-01
5 5.000000e-01 -8.660254e-01 1.000000e+00 -8.660254e-01 5.000000e-01
6 1.224647e-16 -2.449294e-16 3.673940e-16 -4.898587e-16 6.123234e-16 
plot(tmp.data$trend, dt1$sin_12, type='l')

dt2 <- Reduce(cbind.data.frame, lapply(as.list(1:5), function(i) cos(2*pi*i/12*tmp.data_2$trend)))
names(dt2) <- paste("cos", c(12,6,4,3,2.4), sep="_")
tmp.data_3 <- cbind.data.frame(tmp.data_2, dt1, dt2)
head(tmp.data_3)
A data.frame: 6 × 12
lndep trend sin_12 sin_6 sin_4 sin_3 sin_2.4 cos_12 cos_6 cos_4 cos_3 cos_2.4
<dbl> <int> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 6.047372 1 5.000000e-01 8.660254e-01 1.000000e+00 8.660254e-01 5.000000e-01 8.660254e-01 0.5 6.123234e-17 -0.5 -8.660254e-01
2 6.126869 2 8.660254e-01 8.660254e-01 1.224647e-16 -8.660254e-01 -8.660254e-01 5.000000e-01 -0.5 -1.000000e+00 -0.5 5.000000e-01
3 6.408529 3 1.000000e+00 1.224647e-16 -1.000000e+00 -2.449294e-16 1.000000e+00 6.123234e-17 -1.0 -1.836970e-16 1.0 3.061617e-16
4 6.335054 4 8.660254e-01 -8.660254e-01 -2.449294e-16 8.660254e-01 -8.660254e-01 -5.000000e-01 -0.5 1.000000e+00 -0.5 -5.000000e-01
5 6.284134 5 5.000000e-01 -8.660254e-01 1.000000e+00 -8.660254e-01 5.000000e-01 -8.660254e-01 0.5 3.061617e-16 -0.5 8.660254e-01
6 6.284134 6 1.224647e-16 -2.449294e-16 3.673940e-16 -4.898587e-16 6.123234e-16 -1.000000e+00 1.0 -1.000000e+00 1.0 -1.000000e+00

- 모형 적합

\[Z_t = \beta_0 + \beta_1 t + \sum_{i=1}^5 \{ \beta_{1,i} sin \left( \frac{2 \pi ti}{12} \right) + \beta_{2,i} cos \left( \frac{2\pi ti}{12} \right) \}\]

reg_sin <- lm(lndep ~., data=tmp.data_3)
summary(reg_sin)

Call:
lm(formula = lndep ~ ., data = tmp.data_3)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.08232 -0.04855  0.00972  0.04645  0.08527 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)  6.3237250  0.0148062 427.100  < 2e-16 ***
trend        0.0107376  0.0004242  25.315  < 2e-16 ***
sin_12      -0.0277129  0.0103066  -2.689 0.009829 ** 
sin_6       -0.0382551  0.0102107  -3.747 0.000481 ***
sin_4       -0.1555546  0.0101931 -15.261  < 2e-16 ***
sin_3        0.0666506  0.0101872   6.543 3.70e-08 ***
sin_2.4      0.0128922  0.0101849   1.266 0.211691    
cos_12       0.0857900  0.0101931   8.416 5.21e-11 ***
cos_6        0.1675743  0.0101931  16.440  < 2e-16 ***
cos_4        0.1592698  0.0101931  15.625  < 2e-16 ***
cos_3        0.1267107  0.0101931  12.431  < 2e-16 ***
cos_2.4      0.2000603  0.0101931  19.627  < 2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.05578 on 48 degrees of freedom
Multiple R-squared:  0.9796,    Adjusted R-squared:  0.9749 
F-statistic: 209.5 on 11 and 48 DF,  p-value: < 2.2e-16
plot(lndep~tmp.data$day, tmp.data_3,
     main = 'observation vs. fitted value',
     xlab="", ylab="",
     type='l',
     col='skyblue',
     lwd=2, cex.axis=2, cex.main=2) +
 points(lndep~day, tmp.data, col="steelblue", cex=2, pch=16) +
 lines(tmp.data$day, fitted(reg_sin), col='red', lty=2, lwd=2)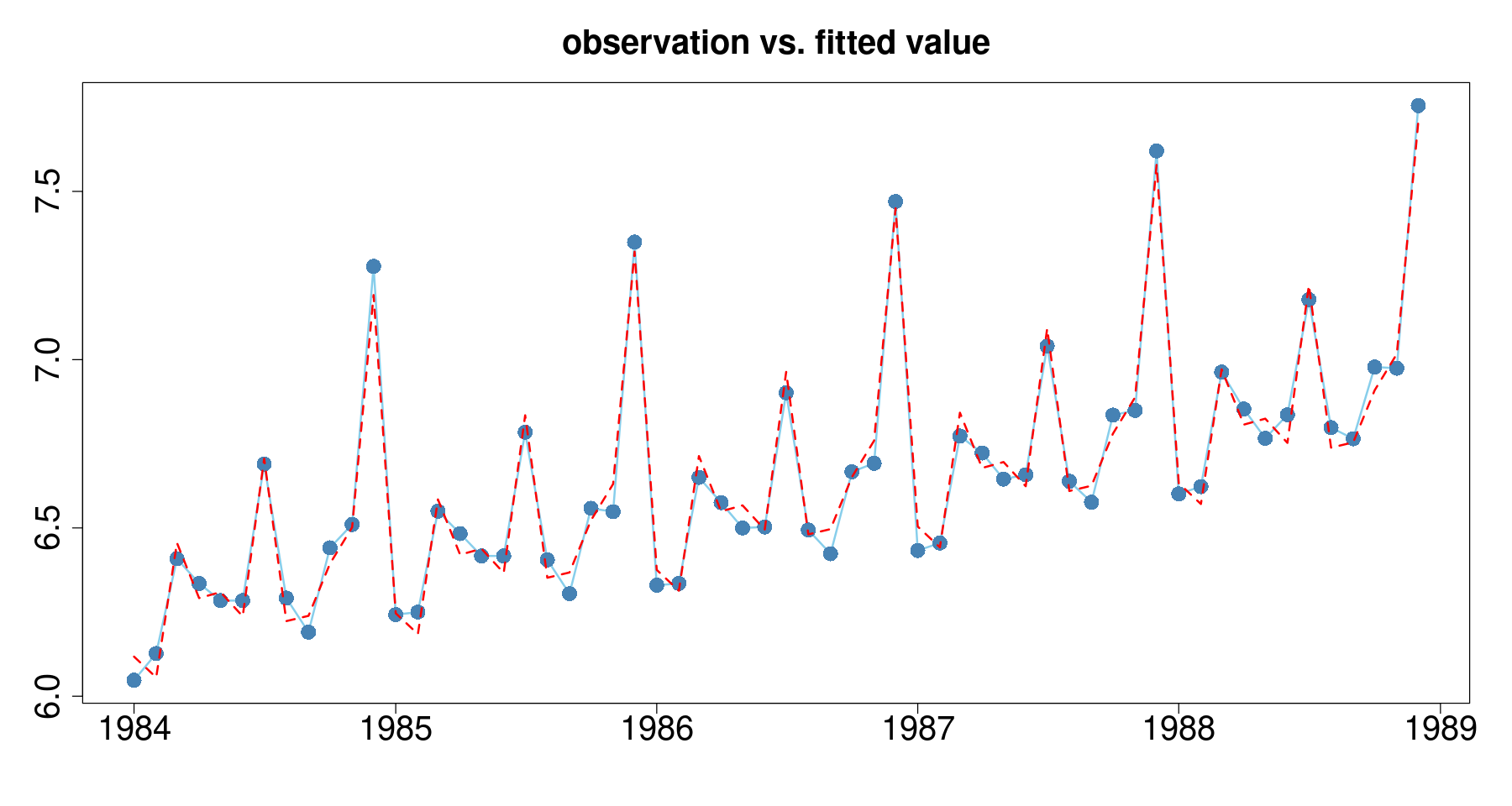

잔차분석

plot(tmp.data$day, resid(reg_sin),
 pch=16, cex=2, xaxt='n', type='b',
 xlab="", ylab="", main="잔차의 시계열 그림", cex.main=2)
abline(h=0, lty=2, lwd=2)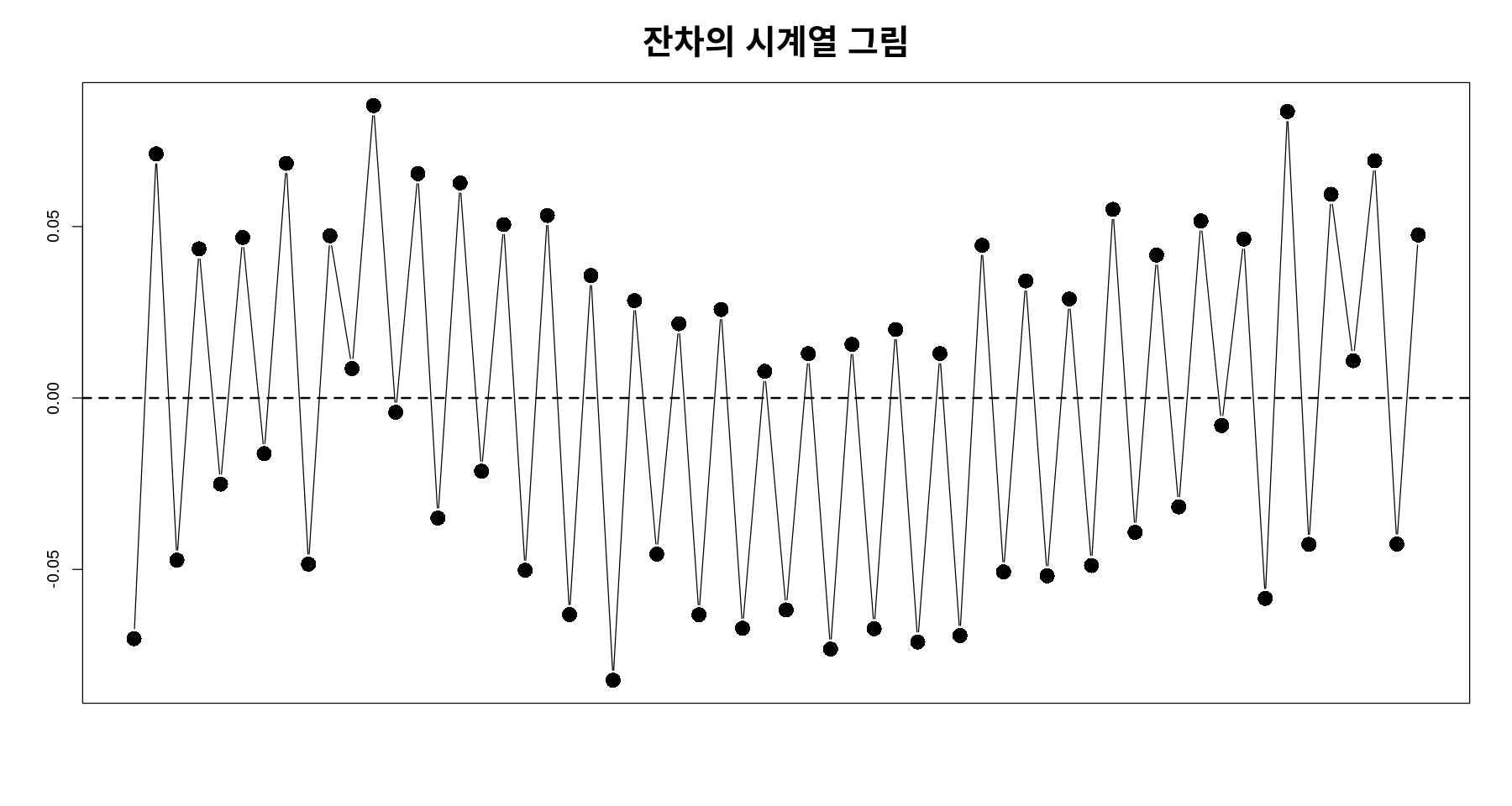

  • 음의 상관관계ㅡ

독립성검정 : DW test

# DW tets
dwtest(reg_sin, alternative = "two.side")

    Durbin-Watson test

data:  reg_sin
DW = 3.2703, p-value = 1.269e-06
alternative hypothesis: true autocorrelation is not 0
dwtest(reg_sin, alternative = "less")

    Durbin-Watson test

data:  reg_sin
DW = 3.2703, p-value = 6.346e-07
alternative hypothesis: true autocorrelation is less than 0
mse_reg_indicator <- sum((z- hat_z)^2)/length(z)
mse_reg_indicator
353.669083494948 
mse_reg_sin <- sum((z- exp(fitted(reg_sin)))^2)/length(z)
mse_reg_sin
1928.97637547109

예측

new_data <- data.frame(
     trend = 61:72,
     y = as.factor(1:12)
     )
new_data
A data.frame: 12 × 2
trend y
<int> <fct>
61 1
62 2
63 3
64 4
65 5
66 6
67 7
68 8
69 9
70 10
71 11
72 12 
predict(reg, newdata = new_data)
1
6.7144672456811
2
6.74173664641499
3
7.05271572206396
4
6.97760319970194
5
6.90615716706365
6
6.92335529591197
7
7.30274501587322
8
6.90918186129912
9
6.83567387691014
10
7.07966982631314
11
7.09859120927279
12
7.87802148673723
exp(predict(reg, newdata = new_data))
1
824.244530071992
2
847.030451690602
3
1155.99384180977
4
1072.34508738392
5
998.403164382383
6
1015.7223324074
7
1484.36895660247
8
1001.42760036959
9
930.455151751132
10
1187.57634730933
11
1210.26086864202
12
2638.64679410606
predict_result <- as.data.frame(predict(reg, newdata = new_data, interval = "predict"))

예측 오차

predict_result$fitted_dep <- exp(predict_result$fit)
predict_result$fitted_dep_l <- exp(predict_result$lwr)
predict_result$fitted_dep_u <- exp(predict_result$upr)
predict_result
A data.frame: 12 × 6
fit lwr upr fitted_dep fitted_dep_l fitted_dep_u
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 6.714467 6.656996 6.771939 824.2445 778.2095 873.0027
2 6.741737 6.684265 6.799208 847.0305 799.7228 897.1365
3 7.052716 6.995244 7.110187 1155.9938 1091.4303 1224.3767
4 6.977603 6.920132 7.035075 1072.3451 1012.4534 1135.7797
5 6.906157 6.848686 6.963629 998.4032 942.6412 1057.4637
6 6.923355 6.865884 6.980827 1015.7223 958.9931 1075.8074
7 7.302745 7.245274 7.360216 1484.3690 1401.4653 1572.1768
8 6.909182 6.851710 6.966653 1001.4276 945.4967 1060.6671
9 6.835674 6.778202 6.893145 930.4552 878.4882 985.4962
10 7.079670 7.022198 7.137141 1187.5763 1121.2489 1257.8274
11 7.098591 7.041120 7.156063 1210.2609 1142.6664 1281.8539
12 7.878021 7.820550 7.935493 2638.6468 2491.2754 2794.7360

점추정/상한/하한. 왼쪽 3개는 로그값이니까 exp취해준 오른쪽 값 3개를 봐야함!

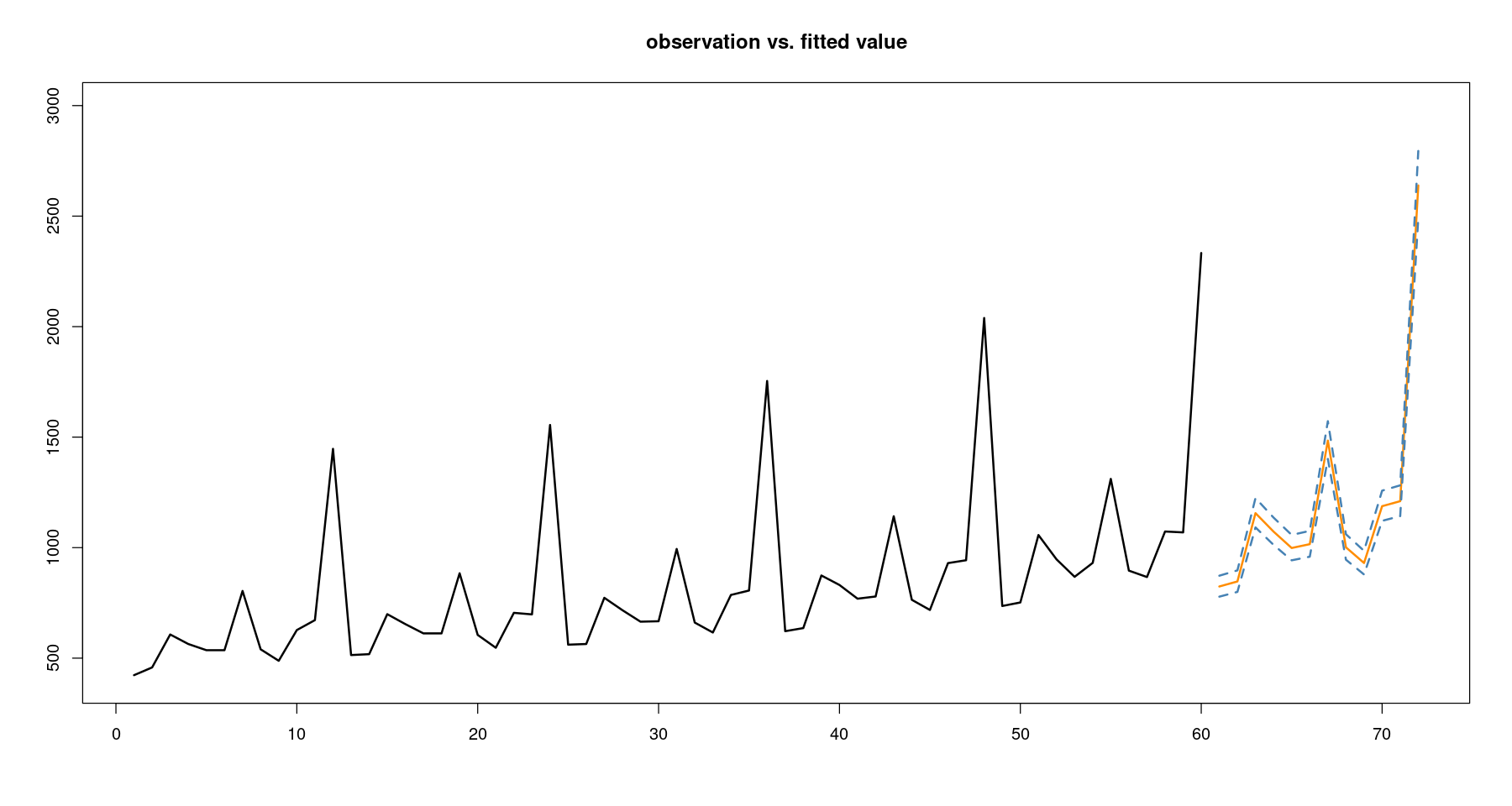
plot(z~tmp.data$trend, tmp.data,
     main = 'observation vs. fitted value',
     xlab="", ylab="",
     xlim=c(1,72),
     ylim=c(400,3000),
     type='l',
     lwd=2)
lines(61:72, predict_result$fitted_dep, col='darkorange', lwd=2)
lines(61:72, predict_result$fitted_dep_l, col='steelblue', lwd=2, lty=2)
lines(61:72, predict_result$fitted_dep_u, col='steelblue', lwd=2, lty=2)